1.11. Himmelblau’s function#
Himmelblau’s function is another famous mathematical function used as a benchmark problem in optimization. It’s named after David Mautner Himmelblau, who introduced it in 1972. The function is defined as follows:

Fig. 1.7 Himmelblau’s function Source: https://commons.wikimedia.org/wiki/File:Himmelblau_function.svg. Image by Morn the Gorn. Released to the public domain#
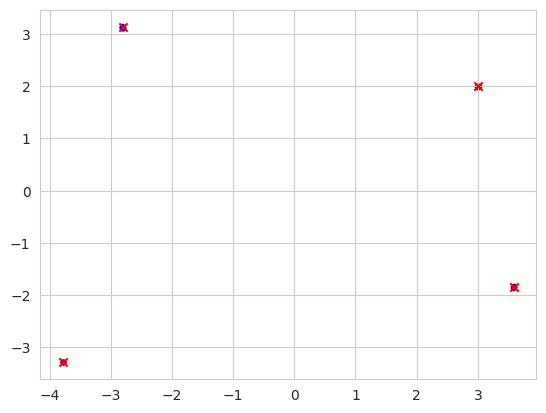
Although this function seems simpler in comparison to the Eggholder function, it draws interest as it is multi-modal, in other words, it has more than one global minimum. To be exact, the function has four global minima evaluating to 0, which can be found in the following locations:
x=3.0, y=2.0
x=−2.805118, y=3.131312
x=−3.779310, y=−3.283186
x=3.584458, y=−1.848126
Which can be despicted here:
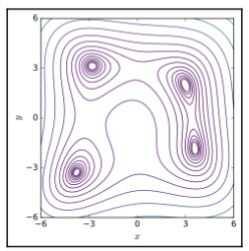
Fig. 1.8 Contour diagram of Himmelblau’s function Source: https://commons.wikimedia.org/wiki/File:Himmelblau_contour.svg. Image by: Nicoguaro. Licensed under Creative Commons CC BY 4.0: https://creativecommons.org/licenses/by/4.0/deed.en.#
Let’s break it down:
The Structure: Himmelblau’s function is made up of two polynomial terms, each squared and added together.
The Variables: The function depends on two variables, ( x ) and ( y ), which represent coordinates on a 2D plane.
The Squares: Each term in the function is squared. Squaring ensures that all parts of the function are positive, which can create multiple local minima and maxima.
The Constants: The numbers 11 and 7 in the function are constants.
The Summation: The squared terms are added together to form a single value, which represents the height of the function’s surface at a given point ( (x,y) ).
The Objective: The goal is to find the minimum value of the function, which corresponds to the lowest point on its surface.
Himmelblau’s function is particularly interesting because it has four identical local minima, each with a value of 0, and one global minimum also at 0. These minima are located at the points:
These points are like valleys in the landscape represented by the function, and finding them can be challenging due to the function’s complex structure with multiple hills and valleys.
In optimization, scientists and engineers use Himmelblau’s function to test and compare different optimization algorithms. The efficiency of an algorithm is measured by how quickly and accurately it can find the global minimum (the lowest point) of the function. If an algorithm can efficiently navigate the landscape of Himmelblau’s function to find the minima, it’s likely to perform well on other optimization problems too.
from deap import base
from deap import creator
from deap import tools
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import elitism
def run_himmelblau_optimization_genetic(DIMENSIONS = 2, BOUND_LOW = -5.0, BOUND_UP = 5.0, POPULATION_SIZE = 300, P_CROSSOVER = 0.9, P_MUTATION = 0.5, MAX_GENERATIONS = 300, HALL_OF_FAME_SIZE = 30, CROWDING_FACTOR = 20.0, RANDOM_SEED = 42):
random.seed(RANDOM_SEED)
toolbox = base.Toolbox()
# define a single objective, minimizing fitness strategy:
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
# create the Individual class based on list:
creator.create("Individual", list, fitness=creator.FitnessMin)
# helper function for creating random float numbers uniformaly distributed within a given range [low, up]
# it assumes that the range is the same for every dimension
def randomFloat(low, up):
return [random.uniform(a, b) for a, b in zip([low] * DIMENSIONS, [up] * DIMENSIONS)]
# create an operator that randomly returns a float in the desired range and dimension:
toolbox.register("attr_float", randomFloat, BOUND_LOW, BOUND_UP)
# create the individual operator to fill up an Individual instance:
toolbox.register("individualCreator", tools.initIterate, creator.Individual, toolbox.attr_float)
# create the population operator to generate a list of individuals:
toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator)
# Himmelblau function as the given individual's fitness:
def himmelblau(individual):
x = individual[0]
y = individual[1]
f = (x ** 2 + y - 11) ** 2 + (x + y ** 2 - 7) ** 2
return f, # return a tuple
toolbox.register("evaluate", himmelblau)
# genetic operators:
toolbox.register("select", tools.selTournament, tournsize=2)
toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR)
toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR, indpb=1.0/DIMENSIONS)
# create initial population (generation 0):
population = toolbox.populationCreator(n=POPULATION_SIZE)
# prepare the statistics object:
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("min", np.min)
stats.register("avg", np.mean)
# define the hall-of-fame object:
hof = tools.HallOfFame(HALL_OF_FAME_SIZE)
# perform the Genetic Algorithm flow with elitism:
population, logbook = elitism.eaSimpleWithElitism(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION,
ngen=MAX_GENERATIONS, stats=stats, halloffame=hof, verbose=True)
# print info for best solution found:
best = hof.items[0]
print("-- Best Individual = ", best)
print("-- Best Fitness = ", best.fitness.values[0])
print("- Best solutions are:")
for i in range(HALL_OF_FAME_SIZE):
print(i, ": ", hof.items[i].fitness.values[0], " -> ", hof.items[i])
# extract statistics:
minFitnessValues, meanFitnessValues = logbook.select("min", "avg")
return minFitnessValues, meanFitnessValues, population
minFitnessValues_42, meanFitnessValues_42, population_42 = run_himmelblau_optimization_genetic(RANDOM_SEED=42)
# random with seed 13 for comparison:
minFitnessValues_13, meanFitnessValues_13, population_13 = run_himmelblau_optimization_genetic(RANDOM_SEED=13)
# plot statistics:
# plot solution locations on x-y plane:
plt.figure(1)
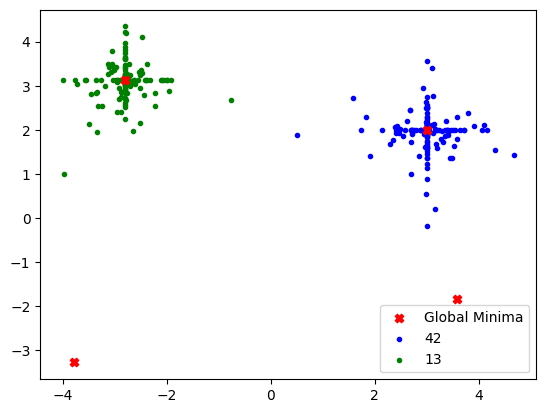
globalMinima = [[3.0, 2.0], [-2.805118, 3.131312], [-3.779310, -3.283186], [3.584458, -1.848126]]
plt.scatter(*zip(*globalMinima), marker='X', color='red', zorder=1)
plt.scatter(*zip(*population_42), marker='.', color='blue', zorder=0)
plt.scatter(*zip(*population_13), marker='.', color='green', zorder=0)
# Legends and labels.
plt.legend(['Global Minima', '42', '13'])
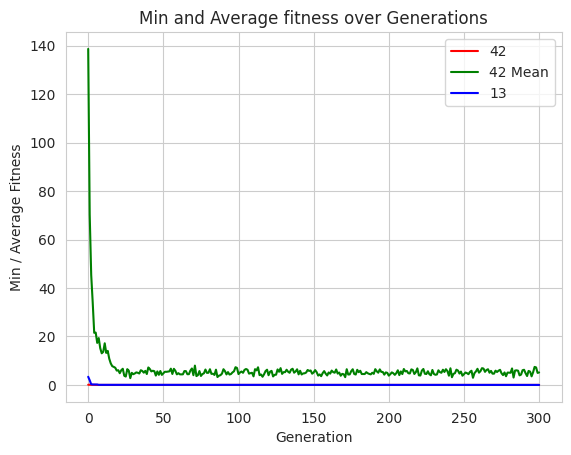
plt.figure(2)
sns.set_style("whitegrid")
plt.plot(minFitnessValues_42, color='red')
plt.plot(meanFitnessValues_42, color='green')
plt.plot(minFitnessValues_13, color='blue')
plt.xlabel('Generation')
plt.ylabel('Min / Average Fitness')
plt.title('Min and Average fitness over Generations')
# Legends.
plt.legend(['42', '42 Mean', '13'])
plt.show()
gen nevals min avg
0 300 0.077887 138.646
1 256 0.077887 70.3018
2 261 0.0549376 45.3529
3 260 0.0549376 34.0376
4 253 0.0421103 21.4902
5 259 0.00375114 21.5907
6 255 0.00163305 17.3338
7 265 0.00163305 19.3309
8 252 0.00163305 15.1737
9 249 0.000356589 13.0519
10 258 0.000356589 13.6612
11 257 0.00027667 17.1779
12 256 0.00027667 13.212
13 255 7.48096e-05 14.0379
14 254 7.48096e-05 10.8216
15 261 2.53197e-05 8.90194
16 258 2.53197e-05 7.73907
17 262 2.53197e-05 7.43993
18 258 2.53197e-05 7.086
19 250 7.19839e-06 5.91175
20 252 4.87197e-06 6.0666
21 256 2.2194e-06 4.83019
22 252 1.41761e-06 6.06226
23 260 1.41761e-06 6.66497
24 258 1.30806e-06 3.77568
25 256 1.30806e-06 3.44466
26 264 6.64878e-08 6.49944
27 255 6.64878e-08 5.88264
28 257 6.64878e-08 2.79407
29 263 6.64878e-08 4.97824
30 252 6.64878e-08 4.42222
31 246 6.09978e-08 4.7264
32 260 6.09978e-08 5.17458
33 255 6.09978e-08 5.00506
34 248 5.92724e-08 4.71614
35 253 4.92809e-08 6.06632
36 250 4.92809e-08 5.75887
37 259 4.92809e-08 5.04934
38 262 6.7185e-09 5.79557
39 255 6.7185e-09 4.49387
40 261 6.7185e-09 7.20528
41 261 6.7185e-09 6.55486
42 248 6.7185e-09 5.58253
43 254 6.7185e-09 5.84513
44 254 6.7185e-09 5.65996
45 255 5.98006e-09 3.85545
46 252 5.83204e-09 5.57192
47 248 4.37779e-09 4.175
48 254 4.37779e-09 5.74221
49 255 4.37779e-09 4.14253
50 250 3.54443e-09 4.78216
51 266 3.35848e-09 5.43377
52 265 8.84248e-10 5.40311
53 252 8.84248e-10 5.49593
54 259 8.84248e-10 5.59
55 260 8.84248e-10 6.70795
56 257 7.94254e-11 4.51569
57 262 7.94254e-11 6.6488
58 257 3.91143e-11 5.81699
59 253 3.91143e-11 4.35297
60 253 3.91143e-11 4.84955
61 258 3.73926e-11 4.36845
62 254 3.73926e-11 4.34962
63 263 6.59053e-12 4.37778
64 257 6.59053e-12 5.70127
65 252 5.27567e-12 5.70112
66 245 5.27567e-12 4.41927
67 254 5.27567e-12 4.43039
68 258 5.27567e-12 5.94242
69 253 4.15001e-12 6.78561
70 254 4.14926e-12 4.00583
71 259 4.14926e-12 7.96415
72 259 4.14926e-12 3.64832
73 257 4.14924e-12 4.02725
74 258 3.82499e-12 5.71551
75 255 3.71594e-12 3.70308
76 260 3.68593e-12 4.48195
77 258 3.68593e-12 4.80197
78 261 3.68593e-12 6.34867
79 259 3.60916e-12 4.97059
80 254 3.47847e-12 5.02246
81 259 3.47802e-12 6.47276
82 262 3.43591e-12 4.55467
83 259 3.43591e-12 4.63276
84 252 9.90117e-13 4.12008
85 266 4.60997e-13 6.28692
86 254 4.48486e-13 3.25242
87 253 4.02874e-13 3.813
88 263 4.02874e-13 4.02812
89 244 2.74599e-14 4.65641
90 263 2.74599e-14 6.48003
91 259 2.74599e-14 5.68404
92 250 2.6433e-14 4.33109
93 253 2.6433e-14 5.2835
94 260 2.46705e-14 4.28592
95 266 8.80552e-15 4.50037
96 255 6.26147e-15 5.16448
97 261 6.26147e-15 5.62274
98 253 6.26147e-15 7.30574
99 263 6.26147e-15 7.00746
100 255 5.2393e-15 4.47544
101 245 4.75521e-15 5.12811
102 263 4.46882e-15 5.52925
103 257 4.46882e-15 4.99727
104 261 4.2743e-15 6.20864
105 254 4.2743e-15 6.55723
106 254 4.2743e-15 6.26547
107 257 4.2743e-15 4.66188
108 256 4.2743e-15 4.86191
109 253 4.2743e-15 5.00868
110 258 4.2606e-15 3.53641
111 259 4.2606e-15 6.48986
112 260 4.18844e-15 5.99779
113 258 1.2422e-15 7.27412
114 263 6.88896e-16 4.03056
115 253 6.88896e-16 4.29077
116 245 6.88896e-16 3.37854
117 262 6.88896e-16 4.38584
118 257 6.88896e-16 5.71372
119 251 6.88563e-16 6.27232
120 253 6.88563e-16 4.00742
121 258 6.88563e-16 5.4352
122 258 6.44992e-16 5.80938
123 254 6.44992e-16 3.50288
124 258 6.44992e-16 4.1607
125 262 6.00234e-16 4.2262
126 260 5.99939e-16 6.38462
127 255 5.0302e-16 5.42886
128 259 4.71991e-16 6.92739
129 261 4.71991e-16 4.55161
130 264 4.71991e-16 5.27377
131 254 4.71991e-16 5.26929
132 255 4.26631e-16 6.26138
133 257 1.51201e-17 5.44689
134 257 1.51201e-17 5.01166
135 256 1.51201e-17 6.2964
136 260 1.51201e-17 6.67106
137 263 1.51201e-17 5.04854
138 258 1.51201e-17 5.56134
139 254 1.51201e-17 6.43982
140 254 1.48309e-17 4.36226
141 251 1.16021e-17 5.83615
142 263 1.16021e-17 4.2999
143 259 1.12847e-17 4.74417
144 255 8.27431e-18 4.79704
145 256 8.27431e-18 5.11907
146 260 8.27431e-18 6.16718
147 259 8.26457e-18 5.76731
148 261 8.26457e-18 5.94955
149 255 5.68786e-18 4.61941
150 255 3.8959e-18 5.16448
151 258 2.10357e-18 6.10652
152 261 1.88468e-18 5.25709
153 258 1.88468e-18 3.84778
154 255 1.67776e-18 4.32516
155 259 1.67776e-18 3.61752
156 253 1.05342e-18 4.86505
157 260 1.05342e-18 5.69881
158 251 1.05342e-18 4.65244
159 256 1.05342e-18 3.90631
160 259 8.62071e-19 5.14928
161 259 8.62071e-19 4.64952
162 255 8.62071e-19 5.91489
163 262 7.74407e-19 5.28551
164 260 7.74407e-19 5.03704
165 251 7.74407e-19 6.37295
166 258 7.74407e-19 4.65555
167 258 7.44463e-19 5.121
168 261 7.44463e-19 3.79476
169 261 7.44463e-19 4.55875
170 253 6.61489e-19 4.39674
171 263 6.61489e-19 3.19968
172 262 6.28569e-19 6.48092
173 258 6.15509e-19 4.28257
174 257 6.15509e-19 4.35274
175 251 6.15509e-19 5.69152
176 251 6.15509e-19 6.46196
177 258 6.15509e-19 4.5042
178 264 6.15509e-19 4.28497
179 252 4.88245e-19 6.24239
180 255 4.88245e-19 5.24948
181 257 4.88161e-19 5.8414
182 242 4.03453e-19 4.49829
183 253 3.76881e-19 4.48822
184 251 1.35374e-19 4.49499
185 257 1.34988e-19 5.26963
186 249 1.31563e-19 4.80943
187 251 5.55449e-20 4.53116
188 252 5.55449e-20 4.35748
189 255 5.55449e-20 5.01843
190 259 5.55449e-20 4.58301
191 260 5.55449e-20 6.50166
192 257 5.55449e-20 5.60903
193 253 3.72329e-20 5.0519
194 259 3.72329e-20 6.40786
195 258 3.72329e-20 5.38253
196 253 3.71331e-20 5.33413
197 255 3.71331e-20 4.24701
198 260 3.71331e-20 5.15569
199 246 3.71331e-20 4.97763
200 251 3.11769e-20 3.8249
201 256 3.11517e-20 4.43029
202 257 3.09194e-20 5.17344
203 256 2.91647e-20 4.81181
204 253 2.84143e-20 4.1455
205 264 2.49659e-20 4.88526
206 265 2.32798e-20 6.04405
207 257 2.32798e-20 4.05233
208 259 2.32798e-20 5.56362
209 257 8.71822e-21 4.47029
210 255 8.61706e-21 6.56248
211 254 8.61706e-21 5.5802
212 254 8.61706e-21 5.76192
213 258 8.36642e-21 4.82376
214 255 5.57846e-21 4.73494
215 257 3.95388e-21 6.41342
216 265 3.61458e-21 6.15599
217 256 2.43816e-21 4.51296
218 249 2.43816e-21 5.26496
219 253 2.43816e-21 6.82017
220 257 2.43816e-21 3.95613
221 257 2.43816e-21 3.88237
222 255 2.43294e-21 5.90369
223 250 2.38002e-21 6.57657
224 261 2.07038e-21 4.6117
225 260 2.07038e-21 4.50432
226 260 1.20233e-21 5.63666
227 255 1.19992e-21 4.41436
228 261 1.19992e-21 3.97916
229 253 1.19992e-21 6.17465
230 255 1.19992e-21 4.52634
231 251 1.19992e-21 4.18371
232 251 1.17164e-21 4.31206
233 258 1.17092e-21 6.02729
234 257 1.17067e-21 5.26325
235 257 1.16985e-21 5.01923
236 251 1.15866e-21 6.26461
237 262 1.12613e-21 5.34563
238 255 7.63154e-22 6.4752
239 261 5.93704e-22 5.7139
240 264 5.93704e-22 3.81185
241 259 5.93704e-22 6.86897
242 259 5.92816e-22 3.18017
243 253 5.92816e-22 4.56788
244 258 5.92816e-22 4.83256
245 262 5.92816e-22 6.29087
246 256 5.75856e-22 5.94374
247 258 5.75856e-22 4.69616
248 259 5.75723e-22 5.50925
249 259 6.3192e-23 3.80087
250 259 6.3192e-23 4.41893
251 254 6.3192e-23 5.11537
252 258 6.3192e-23 4.86276
253 256 6.3192e-23 4.42574
254 253 6.3192e-23 5.3933
255 257 6.08675e-23 5.84683
256 254 6.08675e-23 2.948
257 261 4.66027e-23 4.85923
258 266 4.66027e-23 5.58709
259 258 4.66027e-23 6.65547
260 254 4.66027e-23 5.06172
261 256 4.66027e-23 5.69355
262 262 4.64348e-23 6.90995
263 254 4.63872e-23 6.74979
264 256 4.62394e-23 5.39876
265 256 4.5475e-23 6.16086
266 265 4.5475e-23 6.47227
267 253 4.5475e-23 5.04053
268 262 4.5475e-23 5.78258
269 255 4.54412e-23 4.65128
270 264 4.54412e-23 4.65313
271 261 4.54412e-23 5.89047
272 260 4.54412e-23 5.33603
273 261 4.54412e-23 5.86113
274 250 4.54412e-23 6.23454
275 252 4.53438e-23 4.80711
276 251 3.92798e-23 4.05758
277 260 3.92641e-23 5.14986
278 253 3.87712e-23 3.58922
279 256 3.86246e-23 5.09143
280 246 8.08865e-24 5.05197
281 257 8.08865e-24 5.02208
282 253 8.08865e-24 6.80142
283 251 7.55373e-24 3.03274
284 263 7.55373e-24 5.9319
285 254 7.12276e-24 6.01458
286 254 7.12276e-24 5.86623
287 256 6.94241e-24 3.94701
288 261 6.66183e-24 4.25718
289 260 6.64995e-24 6.06468
290 248 6.64995e-24 6.25063
291 251 6.23736e-24 4.83061
292 248 6.23736e-24 3.67227
293 263 5.38278e-24 5.77907
294 260 5.38278e-24 5.48787
295 255 5.38278e-24 3.54449
296 248 5.38278e-24 5.2204
297 260 4.68039e-24 7.43367
298 251 2.10797e-24 7.20637
299 253 2.10797e-24 4.95986
300 257 2.10797e-24 5.14909
-- Best Individual = [2.9999999999998224, 2.000000000000362]
-- Best Fitness = 2.1079657119389998e-24
- Best solutions are:
0 : 2.1079657119389998e-24 -> [2.9999999999998224, 2.000000000000362]
1 : 2.2357990439082543e-24 -> [2.9999999999998224, 2.000000000000376]
2 : 2.3262466798572746e-24 -> [3.000000000000002, 2.0000000000003686]
3 : 2.4863917545043818e-24 -> [3.0000000000000235, 2.0000000000003673]
4 : 2.6850837284242085e-24 -> [3.0000000000000444, 2.000000000000367]
5 : 2.969177783943262e-24 -> [3.0000000000000644, 2.000000000000371]
6 : 4.277800995813578e-24 -> [2.999999999999644, 2.0000000000003486]
7 : 4.308471907808571e-24 -> [2.999999999999644, 2.0000000000003553]
8 : 4.542254781375344e-24 -> [2.999999999999632, 2.0000000000003553]
9 : 4.608443366767008e-24 -> [2.99999999999963, 2.000000000000362]
10 : 4.680387481323164e-24 -> [2.9999999999996265, 2.000000000000362]
11 : 4.706675482128749e-24 -> [2.9999999999996265, 2.0000000000003673]
12 : 4.8397973376066054e-24 -> [2.9999999999998224, 2.000000000000581]
13 : 5.263674390087201e-24 -> [2.999999999999598, 2.0000000000003553]
14 : 5.336940635520508e-24 -> [2.9999999999995963, 2.000000000000362]
15 : 5.382780553861996e-24 -> [2.999999999999594, 2.000000000000362]
16 : 5.443774490192779e-24 -> [2.9999999999995914, 2.000000000000362]
17 : 5.752484950259254e-24 -> [2.999999999999999, 2.000000000000582]
18 : 5.771079190656219e-24 -> [3.0, 2.0000000000005826]
19 : 5.787651580553102e-24 -> [3.0, 2.0000000000005835]
20 : 5.843784555985913e-24 -> [3.000000000000001, 2.0000000000005858]
21 : 5.8451058980021585e-24 -> [3.0000000000000107, 2.00000000000058]
22 : 5.849687602139682e-24 -> [3.000000000000011, 2.00000000000058]
23 : 5.850208250337128e-24 -> [3.000000000000002, 2.0000000000005853]
24 : 5.858535466052641e-24 -> [3.000000000000002, 2.0000000000005858]
25 : 5.863536844191742e-24 -> [3.0000000000000155, 2.0000000000005778]
26 : 5.866868992655396e-24 -> [3.000000000000002, 2.000000000000586]
27 : 5.876855971715494e-24 -> [3.000000000000011, 2.0000000000005813]
28 : 5.881636468801133e-24 -> [3.000000000000003, 2.000000000000586]
29 : 5.885811120711563e-24 -> [3.000000000000009, 2.000000000000583]
gen nevals min avg
0 300 3.35972 131.705
1 256 1.90913 81.8846
2 255 0.265975 48.9354
3 255 0.177752 34.6479
4 254 0.177752 23.392
5 254 0.177752 21.2792
6 253 0.177752 19.5267
7 248 0.0297201 19.8319
8 253 0.0297201 21.1444
9 252 0.0126402 17.6631
10 254 0.00985532 16.921
11 252 0.00191867 13.9612
12 262 0.000304058 15.7133
13 252 0.000304058 17.4744
14 254 0.000302592 14.7331
15 261 0.000302592 15.9097
16 250 0.000302592 15.5837
17 248 0.000302592 16.643
18 264 7.72395e-05 12.6406
19 254 7.72395e-05 16.6729
20 248 7.72395e-05 12.5159
21 250 5.24536e-05 11.0512
22 257 2.95871e-05 7.82117
23 263 2.95871e-05 10.4046
24 262 2.95871e-05 11.6654
25 249 9.34649e-06 11.0043
26 259 9.34649e-06 8.72941
27 262 9.30573e-06 7.16617
28 263 9.30573e-06 6.6125
29 246 4.77015e-06 7.0472
30 259 3.283e-06 5.48927
31 262 2.45649e-06 7.83438
32 266 2.45649e-06 7.14255
33 264 1.34501e-06 7.79217
34 256 1.34501e-06 5.41112
35 261 7.97788e-07 8.89032
36 259 4.33689e-07 5.16245
37 259 4.33689e-07 6.92172
38 260 2.39012e-07 7.53679
39 257 2.39012e-07 5.83011
40 260 9.88903e-08 6.33394
41 255 9.88903e-08 7.56908
42 260 9.23784e-08 6.77589
43 250 9.23328e-08 6.51679
44 252 9.23328e-08 6.11241
45 263 9.02859e-08 10.4239
46 251 9.02692e-08 5.06779
47 261 2.80432e-08 8.88404
48 259 2.80432e-08 6.08482
49 255 7.83108e-10 5.33418
50 255 7.83108e-10 6.19978
51 259 7.83108e-10 5.16177
52 257 5.29982e-10 6.24265
53 253 5.29982e-10 7.42928
54 260 2.46922e-11 6.86718
55 263 2.46922e-11 8.75532
56 256 2.46922e-11 6.77635
57 266 2.46922e-11 8.66759
58 266 2.46922e-11 6.7659
59 260 1.8884e-11 6.99401
60 248 1.8122e-11 8.37096
61 253 1.20442e-11 6.71521
62 259 1.10707e-11 6.49011
63 255 1.10707e-11 5.35834
64 251 1.10707e-11 5.94653
65 259 1.37406e-12 6.33389
66 251 1.37406e-12 4.88938
67 256 1.04545e-12 5.77744
68 262 1.04545e-12 6.55077
69 252 1.04545e-12 9.31019
70 253 9.46575e-13 5.98201
71 256 9.46575e-13 7.04563
72 253 6.1396e-13 6.34248
73 260 4.86526e-13 7.72951
74 259 4.64426e-13 3.82313
75 260 4.64426e-13 5.38473
76 260 3.51964e-13 8.12941
77 258 3.51964e-13 7.26752
78 260 3.51964e-13 6.66195
79 252 3.47942e-13 6.72551
80 254 2.90237e-13 7.35551
81 250 1.78021e-13 5.54314
82 258 1.78021e-13 6.58239
83 259 1.35224e-13 5.54233
84 251 1.35224e-13 7.05821
85 254 1.20844e-13 6.17379
86 244 1.20844e-13 6.77009
87 261 1.16697e-13 4.99726
88 246 6.65707e-14 8.44783
89 261 6.65707e-14 8.05532
90 254 6.65707e-14 7.65821
91 251 6.54001e-14 5.94519
92 255 6.54001e-14 6.06854
93 249 6.54001e-14 6.81517
94 260 6.54001e-14 4.99955
95 255 6.54001e-14 8.58214
96 261 6.48037e-14 9.59542
97 254 6.35391e-14 6.49097
98 252 6.35391e-14 8.2666
99 257 5.3458e-14 8.73034
100 255 5.32736e-14 7.00506
101 255 5.26542e-14 6.67595
102 256 5.13974e-14 3.38639
103 251 5.13974e-14 6.15123
104 262 4.01284e-15 7.48665
105 261 4.01284e-15 7.32262
106 254 4.01284e-15 6.21507
107 255 4.01284e-15 7.19884
108 258 2.59952e-15 5.34615
109 259 1.88948e-15 5.03262
110 256 1.78367e-15 6.51958
111 256 4.05123e-16 8.124
112 260 4.05123e-16 7.34357
113 244 2.53543e-16 6.30368
114 263 2.53543e-16 6.44179
115 259 2.53543e-16 6.79736
116 259 2.53543e-16 7.24266
117 259 2.43527e-16 8.05971
118 253 1.56581e-16 7.68931
119 257 1.3426e-16 8.51218
120 259 1.3426e-16 7.0655
121 251 9.69829e-17 7.20644
122 252 9.69829e-17 6.19084
123 262 7.61345e-17 7.26602
124 251 4.59978e-17 7.2042
125 259 3.30461e-17 5.97054
126 264 1.01725e-17 7.30965
127 252 1.01389e-17 7.32988
128 247 1.01389e-17 5.9945
129 262 8.72297e-18 7.25127
130 256 8.72297e-18 5.49504
131 258 8.5969e-18 5.60807
132 255 8.5969e-18 6.15457
133 262 8.5969e-18 5.87448
134 264 6.56054e-18 5.53711
135 261 5.92409e-18 6.97649
136 255 4.98721e-18 6.42594
137 259 4.84004e-18 4.98144
138 259 3.88916e-18 6.75089
139 255 3.88916e-18 8.08345
140 250 3.88916e-18 7.06689
141 255 3.88916e-18 6.79558
142 261 3.88916e-18 6.01367
143 254 3.88911e-18 7.65104
144 252 3.88911e-18 5.90826
145 259 3.88263e-18 8.44028
146 254 3.87233e-18 7.95956
147 255 3.58804e-18 8.09544
148 256 3.58804e-18 7.51281
149 255 3.58804e-18 7.99147
150 250 2.24978e-18 6.89058
151 246 2.24978e-18 7.82818
152 255 2.24978e-18 5.33948
153 259 2.24978e-18 6.26302
154 261 2.16324e-18 5.30151
155 255 2.11789e-18 6.95605
156 251 2.09683e-18 7.17331
157 255 2.09683e-18 11.8051
158 258 1.99056e-18 6.59218
159 259 1.99056e-18 6.03195
160 256 1.94501e-18 7.54985
161 244 1.94501e-18 4.34249
162 259 1.94278e-18 3.89028
163 249 1.94278e-18 5.88357
164 254 1.94163e-18 5.96033
165 254 1.93789e-18 6.22414
166 264 1.93774e-18 5.72588
167 257 1.93774e-18 6.91593
168 255 1.93774e-18 7.04103
169 262 1.93774e-18 7.31046
170 256 1.93685e-18 8.22661
171 256 1.91559e-18 6.91761
172 257 1.90592e-18 7.34597
173 253 5.0823e-19 8.15843
174 262 5.08025e-19 7.34421
175 262 5.08025e-19 8.17275
176 256 5.08025e-19 7.35377
177 262 5.08025e-19 6.66899
178 257 5.08025e-19 6.20248
179 254 5.03051e-19 7.73716
180 255 5.03051e-19 5.96824
181 257 5.03051e-19 5.62636
182 259 5.02954e-19 5.51099
183 254 4.90419e-19 7.96762
184 251 4.90419e-19 5.92094
185 255 4.77754e-19 5.79599
186 251 4.77595e-19 5.60364
187 265 4.77585e-19 5.57927
188 249 4.69989e-19 5.26512
189 255 4.4437e-19 5.07196
190 252 4.09264e-19 6.27822
191 261 4.09264e-19 5.74646
192 253 4.09264e-19 9.74087
193 261 4.06355e-19 6.80598
194 257 4.06287e-19 6.71522
195 254 4.0546e-19 8.69995
196 255 4.05167e-19 5.78905
197 250 4.05167e-19 5.5018
198 253 4.03857e-19 5.79457
199 254 4.01593e-19 5.94866
200 251 4.01593e-19 5.43499
201 249 4.01593e-19 5.60869
202 253 4.01593e-19 5.55366
203 247 4.01593e-19 7.12702
204 257 4.01593e-19 5.83665
205 255 4.01589e-19 5.13001
206 255 4.01589e-19 6.6097
207 259 4.01238e-19 6.92252
208 258 4.01156e-19 6.91222
209 256 1.66989e-19 9.67415
210 248 1.66989e-19 4.89261
211 260 1.66989e-19 6.29826
212 259 1.66749e-19 6.08951
213 259 1.66749e-19 7.79635
214 260 1.65285e-19 11.2637
215 263 1.60196e-19 5.92847
216 258 1.60196e-19 7.54245
217 243 1.60196e-19 10.3501
218 259 1.58667e-19 6.73682
219 256 1.58667e-19 5.42762
220 259 1.58667e-19 6.49389
221 263 1.58667e-19 7.09991
222 251 1.58667e-19 7.74504
223 255 3.36858e-20 8.24159
224 258 3.34878e-20 6.66071
225 260 2.50129e-20 5.52411
226 252 2.01406e-20 7.60913
227 257 2.01406e-20 7.32581
228 254 2.01406e-20 6.53484
229 257 2.01406e-20 6.1063
230 261 1.79566e-20 6.33952
231 255 1.79566e-20 6.2471
232 260 1.23683e-20 7.80874
233 256 1.23683e-20 6.0578
234 248 9.06692e-21 5.7183
235 258 9.06692e-21 8.94956
236 247 9.06692e-21 7.84818
237 256 8.84508e-21 6.57898
238 260 8.43193e-21 5.96024
239 257 4.90363e-21 4.89623
240 251 2.55674e-21 9.00758
241 256 2.55674e-21 6.92852
242 261 2.55674e-21 8.07276
243 251 2.2828e-21 6.9992
244 255 2.2828e-21 6.87258
245 258 2.2828e-21 5.06382
246 261 2.2642e-21 7.62386
247 250 2.09475e-21 6.47462
248 252 2.09475e-21 7.64577
249 256 1.93027e-21 5.8076
250 245 1.93027e-21 6.32176
251 255 1.92338e-21 5.59437
252 255 1.57729e-21 6.29478
253 258 1.57729e-21 6.50337
254 262 1.57729e-21 4.09771
255 256 1.57729e-21 5.79421
256 255 1.56906e-21 6.09066
257 262 1.56906e-21 5.88922
258 256 1.49091e-21 7.31839
259 256 1.45303e-21 7.00971
260 257 8.25205e-22 6.45142
261 252 8.25205e-22 5.66843
262 254 8.07696e-22 7.33748
263 254 8.07696e-22 7.09352
264 260 7.95836e-22 7.69431
265 255 7.35414e-22 5.2441
266 251 7.35414e-22 6.56227
267 249 7.35414e-22 6.63325
268 248 7.04587e-22 5.34459
269 252 6.78952e-22 5.7212
270 259 6.78952e-22 7.3687
271 260 6.78952e-22 7.10475
272 258 6.7624e-22 7.79338
273 252 5.97989e-22 8.34275
274 259 5.97989e-22 9.81208
275 245 5.97989e-22 7.36142
276 258 5.97642e-22 6.93605
277 261 5.9328e-22 6.82679
278 258 5.9328e-22 7.48412
279 251 4.37388e-22 9.4325
280 257 4.37388e-22 7.72123
281 252 3.67229e-22 7.10638
282 261 3.67229e-22 5.32775
283 256 3.67229e-22 7.55916
284 264 3.65143e-22 5.68353
285 262 3.65143e-22 8.26374
286 257 2.024e-22 6.13374
287 249 6.72805e-23 6.40791
288 263 6.72805e-23 8.1572
289 259 6.72805e-23 6.92785
290 248 6.72805e-23 7.0532
291 256 6.66648e-23 7.03569
292 257 6.66648e-23 4.84079
293 263 6.59256e-23 7.85401
294 254 6.59256e-23 5.99407
295 255 6.59256e-23 6.31855
296 255 6.58241e-23 6.59125
297 262 6.42362e-23 6.09981
298 250 6.42362e-23 7.71956
299 267 5.95203e-23 7.82994
300 259 5.91057e-23 5.10117
-- Best Individual = [-2.805118086954073, 3.131312518250381]
-- Best Fitness = 5.910570309082829e-23
- Best solutions are:
0 : 5.910570309082829e-23 -> [-2.805118086954073, 3.131312518250381]
1 : 5.952029051728901e-23 -> [-2.805118086954078, 3.131312518250381]
2 : 6.302102486727553e-23 -> [-2.805118086954135, 3.131312518250507]
3 : 6.357710554114031e-23 -> [-2.805118086954136, 3.1313125182504598]
4 : 6.423617673934712e-23 -> [-2.8051180869541352, 3.131312518250404]
5 : 6.429476464991698e-23 -> [-2.8051180869541357, 3.131312518250404]
6 : 6.472412191910614e-23 -> [-2.8051180869541406, 3.131312518250404]
7 : 6.487655508954381e-23 -> [-2.805118086954143, 3.131312518250409]
8 : 6.495953063499858e-23 -> [-2.805118086954143, 3.131312518250404]
9 : 6.496379995021763e-23 -> [-2.805118086954146, 3.1313125182504202]
10 : 6.49854628595359e-23 -> [-2.8051180869541392, 3.13131251825038]
11 : 6.50379820631619e-23 -> [-2.8051180869541517, 3.1313125182504558]
12 : 6.505389496534202e-23 -> [-2.805118086954148, 3.131312518250428]
13 : 6.508822540307633e-23 -> [-2.8051180869541406, 3.131312518250382]
14 : 6.515460015964163e-23 -> [-2.805118086954158, 3.131312518250507]
15 : 6.521394774326321e-23 -> [-2.805118086954146, 3.131312518250404]
16 : 6.525470660851417e-23 -> [-2.805118086954149, 3.1313125182504202]
17 : 6.526159494193856e-23 -> [-2.8051180869541352, 3.1313125182503456]
18 : 6.531486829658995e-23 -> [-2.8051180869541352, 3.1313125182503434]
19 : 6.535119691899719e-23 -> [-2.8051180869541437, 3.131312518250382]
20 : 6.538869621098777e-23 -> [-2.8051180869541437, 3.13131251825038]
21 : 6.541356110672034e-23 -> [-2.805118086954158, 3.131312518250474]
22 : 6.554277967843916e-23 -> [-2.805118086954154, 3.131312518250431]
23 : 6.555978120866849e-23 -> [-2.805118086954146, 3.1313125182503825]
24 : 6.558073650975478e-23 -> [-2.805118086954154, 3.1313125182504287]
25 : 6.582413480889529e-23 -> [-2.8051180869541485, 3.1313125182503816]
26 : 6.592557601041947e-23 -> [-2.8051180869541574, 3.131312518250428]
27 : 6.592876695278109e-23 -> [-2.80511808695415, 3.131312518250382]
28 : 6.594497567780066e-23 -> [-2.805118086954158, 3.1313125182504282]
29 : 6.596554049273887e-23 -> [-2.805118086954155, 3.1313125182504096]
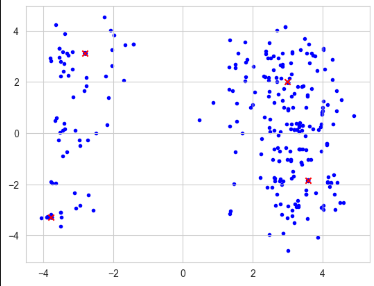
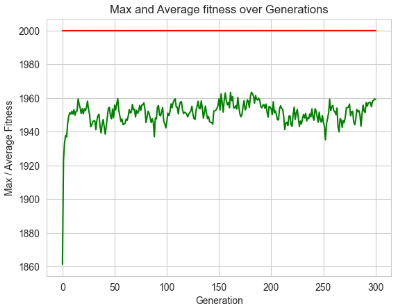
1.12. Using Niching and sharing to find Multiple Solutions#
1.12.1. TASK Complete the following method so that the following implementaiton: for optimizeHimmelblauSharing#
globalMaxima, population, hof, logbook, maxFitnessValues, meanFitnessValues = optimizeHimmelblauSharing()
# plot solution locations on x-y plane:
plt.figure(1)
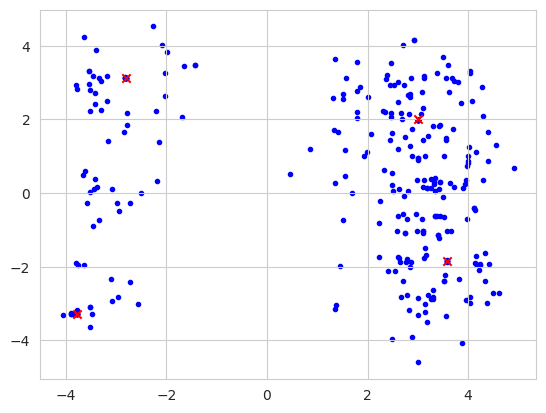
plt.scatter(*zip(*globalMaxima), marker='x', color='red', zorder=1)
plt.scatter(*zip(*population), marker='.', color='blue', zorder=0) # plot solution locations on x-y plane:
# plot best solutions locations on x-y plane:
plt.figure(2)
plt.scatter(*zip(*globalMaxima), marker='x', color='red', zorder=1)
plt.scatter(*zip(*hof.items), marker='.', color='blue', zorder=0)
# extract statistics:
# plot statistics:
plt.figure(3)
sns.set_style("whitegrid")
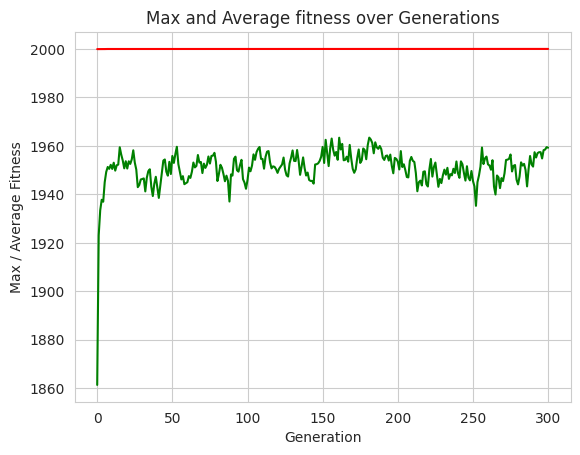
plt.plot(maxFitnessValues, color='red')
plt.plot(meanFitnessValues, color='green')
plt.xlabel('Generation')
plt.ylabel('Max / Average Fitness')
plt.title('Max and Average fitness over Generations')
plt.show()
Use the following base code
1.12.2. Base Code#
from deap import base
from deap import creator
from deap import tools
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import elitism
def optimizeHimmelblauSharing(DIMENSIONS = 2, BOUND_LOW = -5.0, BOUND_UP = 5.0, POPULATION_SIZE = 300, P_CROSSOVER = 0.9, P_MUTATION = 0.5, MAX_GENERATIONS = 300, HALL_OF_FAME_SIZE = 30, CROWDING_FACTOR = 20.0, DISTANCE_THRESHOLD = 0.1, SHARING_EXTENT = 5.0, RANDOM_SEED = 42):
random.seed(RANDOM_SEED)
toolbox = base.Toolbox()
# define a single objective, maximizing fitness strategy:
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
# create the Individual class based on list:
creator.create("Individual", list, fitness=creator.FitnessMax)
# helper function for creating random float numbers uniformaly distributed within a given range [low, up]
# it assumes that the range is the same for every dimension
def randomFloat(low, up):
return [random.uniform(a, b) for a, b in zip([low] * DIMENSIONS, [up] * DIMENSIONS)]
# create an operator that randomly returns a float in the desired range and dimension:
toolbox.register("attr_float", randomFloat, BOUND_LOW, BOUND_UP)
# create the individual operator to fill up an Individual instance:
toolbox.register("individualCreator", tools.initIterate, creator.Individual, toolbox.attr_float)
# create the population operator to generate a list of individuals:
toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator)
# 'Inverted' Himmelblau function as the given individual's fitness:
def himmelblauInverted(individual):
x = individual[0]
y = individual[1]
f = (x ** 2 + y - 11) ** 2 + (x + y ** 2 - 7) ** 2
return 2000.0 - f, # return a tuple
toolbox.register("evaluate", himmelblauInverted)
# TODO Cp,[;ete wraps the tools.selTournament() with fitness sharing
# same signature as tools.selTournament()
def selTournamentWithSharing(individuals, k, tournsize, fit_attr="fitness"):
# get orig fitnesses:
origFitnesses = [ind.fitness.values[0] for ind in individuals]
# TODO Iterate over each individual, calculate the sharingSum as the sum of (1 - distance / (SHARING_EXTENT * DISTANCE_THRESHOLD)) each time the distance is less than the treshhold
# Distance calulcates as: math.sqrt(((individuals[i][0] - individuals[j][0]) ** 2) + ((individuals[i][1] - individuals[j][1]) ** 2))
# apply sharing to each individual:
for i in range(len(individuals)):
sharingSum = 1
# reduce fitness accordingly:
individuals[i].fitness.values = origFitnesses[i] / sharingSum,
# apply original tools.selTournament() using modified fitness:
selected = tools.selTournament(individuals, k, tournsize, fit_attr)
# retrieve original fitness:
for i, ind in enumerate(individuals):
ind.fitness.values = origFitnesses[i],
return selected
# TODO REWRITE Implement genetic operators: as:
# - Tournament selection with sharing torunament size 2
# - Simulated Binary Crossover (SBX) with eta = CROWDING_FACTOR
# - Polynomial mutation with eta = CROWDING_FACTOR
# toolbox.register("select", selTournamentWithSharing, tournsize=2)
# toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR)
# toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR, indpb=1.0/DIMENSIONS)
# create initial population (generation 0):
population = toolbox.populationCreator(n=POPULATION_SIZE)
# prepare the statistics object:
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("max", np.max)
stats.register("avg", np.mean)
# define the hall-of-fame object:
hof = tools.HallOfFame(HALL_OF_FAME_SIZE)
# perform the Genetic Algorithm flow with elitism:
population, logbook = elitism.eaSimpleWithElitism(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION,
ngen=MAX_GENERATIONS, stats=stats, halloffame=hof, verbose=True)
# print info for best solution found:
best = hof.items[0]
print("-- Best Individual = ", best)
print("-- Best Fitness = ", best.fitness.values[0])
print("- Best solutions are:")
for i in range(HALL_OF_FAME_SIZE):
print(i, ": ", hof.items[i].fitness.values[0], " -> ", hof.items[i])
globalMaxima = [[3.0, 2.0], [-2.805118, 3.131312], [-3.779310, -3.283186], [3.584458, -1.848126]]
maxFitnessValues, meanFitnessValues = logbook.select("max", "avg")
return globalMaxima, population, hof, logbook, maxFitnessValues, meanFitnessValues
if __name__ == "__main__":
globalMaxima, population, hof, logbook, maxFitnessValues, meanFitnessValues = optimizeHimmelblauSharing()
# plot solution locations on x-y plane:
plt.figure(1)
# TODO Rewrite the following code to plot the solutions and the global maxima
# plt.scatter(*zip(*globalMaxima), marker='x', color='red', zorder=1)
# plt.scatter(*zip(*population), marker='.', color='blue', zorder=0) # plot solution locations on x-y plane:
# plot best solutions locations on x-y plane:
plt.figure(2)
plt.scatter(*zip(*globalMaxima), marker='x', color='red', zorder=1)
plt.scatter(*zip(*hof.items), marker='.', color='blue', zorder=0)
# extract statistics:
# TODO Rewrite plot statistics:
plt.figure(3)
sns.set_style("whitegrid")
# plt.plot(maxFitnessValues, color='red')
# plt.plot(meanFitnessValues, color='green')
# plt.xlabel('Generation')
# plt.ylabel('Max / Average Fitness')
# plt.title('Max and Average fitness over Generations')
plt.show()
1.12.3. Solution#
from deap import base
from deap import creator
from deap import tools
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import elitism
def optimizeHimmelblauSharing(DIMENSIONS = 2, BOUND_LOW = -5.0, BOUND_UP = 5.0, POPULATION_SIZE = 300, P_CROSSOVER = 0.9, P_MUTATION = 0.5, MAX_GENERATIONS = 300, HALL_OF_FAME_SIZE = 30, CROWDING_FACTOR = 20.0, DISTANCE_THRESHOLD = 0.1, SHARING_EXTENT = 5.0, RANDOM_SEED = 42):
random.seed(RANDOM_SEED)
toolbox = base.Toolbox()
# define a single objective, maximizing fitness strategy:
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
# create the Individual class based on list:
creator.create("Individual", list, fitness=creator.FitnessMax)
# helper function for creating random float numbers uniformaly distributed within a given range [low, up]
# it assumes that the range is the same for every dimension
def randomFloat(low, up):
return [random.uniform(a, b) for a, b in zip([low] * DIMENSIONS, [up] * DIMENSIONS)]
# create an operator that randomly returns a float in the desired range and dimension:
toolbox.register("attr_float", randomFloat, BOUND_LOW, BOUND_UP)
# create the individual operator to fill up an Individual instance:
toolbox.register("individualCreator", tools.initIterate, creator.Individual, toolbox.attr_float)
# create the population operator to generate a list of individuals:
toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator)
# 'Inverted' Himmelblau function as the given individual's fitness:
def himmelblauInverted(individual):
x = individual[0]
y = individual[1]
f = (x ** 2 + y - 11) ** 2 + (x + y ** 2 - 7) ** 2
return 2000.0 - f, # return a tuple
toolbox.register("evaluate", himmelblauInverted)
# wraps the tools.selTournament() with fitness sharing
# same signature as tools.selTournament()
def selTournamentWithSharing(individuals, k, tournsize, fit_attr="fitness"):
# get orig fitnesses:
origFitnesses = [ind.fitness.values[0] for ind in individuals]
# apply sharing to each individual:
for i in range(len(individuals)):
sharingSum = 1
# iterate over all other individuals
for j in range(len(individuals)):
if i != j:
# calculate eucledean distance between individuals:
distance = math.sqrt(
((individuals[i][0] - individuals[j][0]) ** 2) + ((individuals[i][1] - individuals[j][1]) ** 2))
if distance < DISTANCE_THRESHOLD:
sharingSum += (1 - distance / (SHARING_EXTENT * DISTANCE_THRESHOLD))
# reduce fitness accordingly:
individuals[i].fitness.values = origFitnesses[i] / sharingSum,
# apply original tools.selTournament() using modified fitness:
selected = tools.selTournament(individuals, k, tournsize, fit_attr)
# retrieve original fitness:
for i, ind in enumerate(individuals):
ind.fitness.values = origFitnesses[i],
return selected
# genetic operators:
toolbox.register("select", selTournamentWithSharing, tournsize=2)
toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR)
toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR, indpb=1.0/DIMENSIONS)
# create initial population (generation 0):
population = toolbox.populationCreator(n=POPULATION_SIZE)
# prepare the statistics object:
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("max", np.max)
stats.register("avg", np.mean)
# define the hall-of-fame object:
hof = tools.HallOfFame(HALL_OF_FAME_SIZE)
# perform the Genetic Algorithm flow with elitism:
population, logbook = elitism.eaSimpleWithElitism(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION,
ngen=MAX_GENERATIONS, stats=stats, halloffame=hof, verbose=True)
# print info for best solution found:
best = hof.items[0]
print("-- Best Individual = ", best)
print("-- Best Fitness = ", best.fitness.values[0])
print("- Best solutions are:")
for i in range(HALL_OF_FAME_SIZE):
print(i, ": ", hof.items[i].fitness.values[0], " -> ", hof.items[i])
globalMaxima = [[3.0, 2.0], [-2.805118, 3.131312], [-3.779310, -3.283186], [3.584458, -1.848126]]
maxFitnessValues, meanFitnessValues = logbook.select("max", "avg")
return globalMaxima, population, hof, logbook, maxFitnessValues, meanFitnessValues
if __name__ == "__main__":
globalMaxima, population, hof, logbook, maxFitnessValues, meanFitnessValues = optimizeHimmelblauSharing()
# plot solution locations on x-y plane:
plt.figure(1)
plt.scatter(*zip(*globalMaxima), marker='x', color='red', zorder=1)
plt.scatter(*zip(*population), marker='.', color='blue', zorder=0) # plot solution locations on x-y plane:
# plot best solutions locations on x-y plane:
plt.figure(2)
plt.scatter(*zip(*globalMaxima), marker='x', color='red', zorder=1)
plt.scatter(*zip(*hof.items), marker='.', color='blue', zorder=0)
# extract statistics:
# plot statistics:
plt.figure(3)
sns.set_style("whitegrid")
plt.plot(maxFitnessValues, color='red')
plt.plot(meanFitnessValues, color='green')
plt.xlabel('Generation')
plt.ylabel('Max / Average Fitness')
plt.title('Max and Average fitness over Generations')
plt.show()
gen nevals max avg
0 300 1999.92 1861.35
1 256 1999.92 1923.09
2 261 1999.95 1933.39
3 260 1999.95 1937.75
4 257 1999.95 1936.95
5 254 1999.95 1945.01
6 253 1999.97 1949.24
7 257 1999.97 1951.29
8 253 1999.97 1950.51
9 255 1999.97 1952.18
10 252 1999.97 1950.47
11 259 1999.97 1953.05
12 254 1999.97 1949.78
13 263 1999.98 1952.01
14 262 1999.98 1952.26
15 254 1999.98 1959.42
16 256 1999.98 1956.38
17 253 1999.98 1953.97
18 260 1999.98 1950.71
19 258 1999.98 1953.67
20 250 1999.98 1950.64
21 261 1999.98 1953.63
22 256 1999.98 1952.55
23 262 1999.98 1954.43
24 252 1999.98 1958.17
25 259 1999.98 1953.15
26 253 1999.98 1950.21
27 257 1999.98 1942.96
28 243 1999.98 1943.85
29 258 1999.98 1946.13
30 255 1999.98 1946.32
31 250 1999.98 1946.58
32 255 1999.98 1941.21
33 256 1999.98 1946.83
34 251 1999.98 1949.55
35 257 1999.98 1950.34
36 262 2000 1943.15
37 251 2000 1939.29
38 255 2000 1944.38
39 255 2000 1947.25
40 262 2000 1942.93
41 259 2000 1938.53
42 256 2000 1943.79
43 250 2000 1948.97
44 250 2000 1953.92
45 251 2000 1954.38
46 256 2000 1949.33
47 253 2000 1947.69
48 258 2000 1953.4
49 255 2000 1948.38
50 262 2000 1955.83
51 265 2000 1952.95
52 255 2000 1956.61
53 248 2000 1959.61
54 259 2000 1952.47
55 258 2000 1949.38
56 261 2000 1946.14
57 259 2000 1947.51
58 258 2000 1944.19
59 260 2000 1944.61
60 257 2000 1945.01
61 260 2000 1947.51
62 261 2000 1946.78
63 251 2000 1949.29
64 259 2000 1953.12
65 258 2000 1951.11
66 250 2000 1951.7
67 254 2000 1956.22
68 252 2000 1953.08
69 258 2000 1953.34
70 260 2000 1948.78
71 262 2000 1952.67
72 257 2000 1950.9
73 246 2000 1952.19
74 256 2000 1955.62
75 254 2000 1952.69
76 257 2000 1955.85
77 251 2000 1955.95
78 254 2000 1957.12
79 256 2000 1953.45
80 255 2000 1945.5
81 255 2000 1948.48
82 255 2000 1952.19
83 258 2000 1950.96
84 263 2000 1948.38
85 252 2000 1945.4
86 257 2000 1947.7
87 256 2000 1945.62
88 259 2000 1937.03
89 266 2000 1948.2
90 251 2000 1947.72
91 250 2000 1954.68
92 254 2000 1955.54
93 255 2000 1949.94
94 253 2000 1949.36
95 255 2000 1952.04
96 255 2000 1954.24
97 264 2000 1946.26
98 251 2000 1944.85
99 249 2000 1942.29
100 256 2000 1945.86
101 252 2000 1951.03
102 257 2000 1949.52
103 261 2000 1951.86
104 250 2000 1956.49
105 257 2000 1954.23
106 250 2000 1957.38
107 261 2000 1958.75
108 253 2000 1959.53
109 254 2000 1954.64
110 255 2000 1954.6
111 261 2000 1950.58
112 253 2000 1955.47
113 252 2000 1957.61
114 260 2000 1957.86
115 258 2000 1953.17
116 249 2000 1950.72
117 260 2000 1951.55
118 260 2000 1951.33
119 265 2000 1950.36
120 263 2000 1948.85
121 255 2000 1950.53
122 259 2000 1951.45
123 254 2000 1952.32
124 258 2000 1955.17
125 260 2000 1950.18
126 253 2000 1947.85
127 247 2000 1947.34
128 258 2000 1952.78
129 254 2000 1955.12
130 266 2000 1958.12
131 258 2000 1953.8
132 253 2000 1953.73
133 257 2000 1958.29
134 253 2000 1953.94
135 253 2000 1948.05
136 255 2000 1951.48
137 253 2000 1955.23
138 256 2000 1950.82
139 257 2000 1947.76
140 255 2000 1948.98
141 257 2000 1945.92
142 253 2000 1945.52
143 254 2000 1945.56
144 253 2000 1944.41
145 260 2000 1952.31
146 262 2000 1952.43
147 248 2000 1952.78
148 264 2000 1953.78
149 260 2000 1955.5
150 260 2000 1959.57
151 253 2000 1952.94
152 251 2000 1962.49
153 260 2000 1957.03
154 254 2000 1951.66
155 257 2000 1958.87
156 255 2000 1963.01
157 242 2000 1958.38
158 258 2000 1955.95
159 260 2000 1957.48
160 264 2000 1954.25
161 256 2000 1963.36
162 254 2000 1958.49
163 257 2000 1960.82
164 259 2000 1954.04
165 249 2000 1954.21
166 257 2000 1955.53
167 261 2000 1953.48
168 257 2000 1960.39
169 259 2000 1954.86
170 257 2000 1950.54
171 259 2000 1948.89
172 257 2000 1950.3
173 258 2000 1954.98
174 254 2000 1958.5
175 249 2000 1952.96
176 260 2000 1953.99
177 252 2000 1958.91
178 263 2000 1958.23
179 262 2000 1954.48
180 262 2000 1960.33
181 259 2000 1963.4
182 244 2000 1962.66
183 259 2000 1961.2
184 250 2000 1956.94
185 261 2000 1961.46
186 249 2000 1959.38
187 253 2000 1958.77
188 263 2000 1959.94
189 257 2000 1958.68
190 254 2000 1955.1
191 260 2000 1954.18
192 253 2000 1955.86
193 260 2000 1956.02
194 253 2000 1953.93
195 259 2000 1956.4
196 255 2000 1951.74
197 252 2000 1948.69
198 260 2000 1955.03
199 246 2000 1954.61
200 262 2000 1953.52
201 261 2000 1950.27
202 252 2000 1957.84
203 245 2000 1951.27
204 249 2000 1952.39
205 258 2000 1950.02
206 258 2000 1947.14
207 252 2000 1946.98
208 249 2000 1953.81
209 264 2000 1955.42
210 256 2000 1953.83
211 247 2000 1953.36
212 253 2000 1948.79
213 256 2000 1941.27
214 258 2000 1944.99
215 259 2000 1945.66
216 258 2000 1943.64
217 262 2000 1949.3
218 255 2000 1949.5
219 260 2000 1944.16
220 255 2000 1943.23
221 251 2000 1950.27
222 255 2000 1954.58
223 265 2000 1947.32
224 247 2000 1951.27
225 252 2000 1953.11
226 255 2000 1948.05
227 259 2000 1943.11
228 258 2000 1946.37
229 259 2000 1944.65
230 259 2000 1947.86
231 251 2000 1950.19
232 260 2000 1948.1
233 255 2000 1950.94
234 255 2000 1946.37
235 257 2000 1948.32
236 257 2000 1947.84
237 257 2000 1950.55
238 247 2000 1948.79
239 252 2000 1953.55
240 258 2000 1948.76
241 256 2000 1946.79
242 257 2000 1953.6
243 248 2000 1952.4
244 259 2000 1948.79
245 262 2000 1945.68
246 247 2000 1951.59
247 258 2000 1946.88
248 244 2000 1945.76
249 254 2000 1949.63
250 258 2000 1945.53
251 258 2000 1943.26
252 253 2000 1935.25
253 248 2000 1945.02
254 256 2000 1947.76
255 257 2000 1951.44
256 251 2000 1959.32
257 256 2000 1952.49
258 252 2000 1954.82
259 255 2000 1955.57
260 256 2000 1952.37
261 254 2000 1951.89
262 261 2000 1950.14
263 263 2000 1954.08
264 261 2000 1943.19
265 255 2000 1939.92
266 255 2000 1947.77
267 261 2000 1947.01
268 268 2000 1942.56
269 252 2000 1946.69
270 259 2000 1945.47
271 261 2000 1948.67
272 257 2000 1954.17
273 254 2000 1954.31
274 255 2000 1954.64
275 247 2000 1956.44
276 261 2000 1949.43
277 261 2000 1951.77
278 256 2000 1952.08
279 256 2000 1946.05
280 251 2000 1944.09
281 247 2000 1947.33
282 254 2000 1953.2
283 258 2000 1951.87
284 257 2000 1952.57
285 252 2000 1950.02
286 257 2000 1943.27
287 252 2000 1950.36
288 256 2000 1955.81
289 248 2000 1952.33
290 248 2000 1951.44
291 249 2000 1957.38
292 262 2000 1955.19
293 253 2000 1957.01
294 250 2000 1957.39
295 259 2000 1957.39
296 259 2000 1954.79
297 251 2000 1958.22
298 255 2000 1958.45
299 255 2000 1959.46
300 255 2000 1959.24
-- Best Individual = [3.001612371389449, 1.9958270919300878]
-- Best Fitness = 1999.9997428476076
- Best solutions are:
0 : 1999.9997428476076 -> [3.001612371389449, 1.9958270919300878]
1 : 1999.9995532774788 -> [3.585506608049694, -1.8432407550446581]
2 : 1999.9988186889173 -> [3.585506608049694, -1.8396197402430106]
3 : 1999.9987642838498 -> [-3.7758887140006174, -3.2858043455406367]
4 : 1999.9986563457114 -> [-2.8072634380293766, 3.125893564009283]
5 : 1999.9986041717466 -> [2.994996723403235, 1.9969095906576606]
6 : 1999.9984781347296 -> [-3.7758887140006174, -3.2865929477968665]
7 : 1999.998183039951 -> [3.002584526988128, 1.9887182479605638]
8 : 1999.9977631768973 -> [-2.8134037927300475, 3.1316482961709218]
9 : 1999.997575148785 -> [2.9929626808487773, 1.9969095906576606]
10 : 1999.997357526559 -> [-3.7836524052424725, -3.2784944170067725]
11 : 1999.9967191974722 -> [3.002584526988128, 1.984978412500066]
12 : 1999.9965015373687 -> [-3.7758887140006174, -3.2740097495009586]
13 : 1999.9962546878492 -> [-3.7836524052424725, -3.276699727801961]
14 : 1999.9960047913273 -> [3.0041543184731654, 1.983221511075004]
15 : 1999.9959650903231 -> [3.5764734725338276, -1.8389268636893863]
16 : 1999.9958485029426 -> [3.011395294421638, 1.9956529440390214]
17 : 1999.9958037403092 -> [-2.8134037927300475, 3.138421416525262]
18 : 1999.9955679433144 -> [3.011577483310753, 1.9969727049693808]
19 : 1999.9955201658709 -> [-2.8150770882393985, 3.125893564009283]
20 : 1999.9945825944897 -> [-2.8034140680901345, 3.119760103397938]
21 : 1999.994541638767 -> [2.992870437290974, 1.989058665162832]
22 : 1999.9944703022825 -> [-2.8072634380293766, 3.119760103397938]
23 : 1999.9943375904743 -> [-2.8080073292249974, 3.119760103397938]
24 : 1999.9942313466163 -> [-3.7839981775897114, -3.27447808441823]
25 : 1999.9938882116498 -> [-2.8000299644229902, 3.119760103397938]
26 : 1999.993860667051 -> [3.585506608049694, -1.8279194784346149]
27 : 1999.9938265970718 -> [-2.813249891412572, 3.141426924604424]
28 : 1999.993823934265 -> [-2.809941282926521, 3.119760103397938]
29 : 1999.993698362676 -> [3.582334333642025, -1.8678936251244889]