1.10. Chromosomes and genetic operators for real numbers#
We will focus on number representation and genetic operators for real numbers.
1.10.1. Eggholder Function#
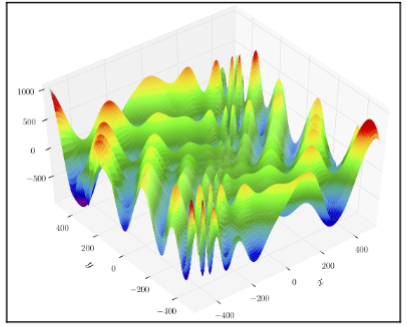
Fig. 1.5 he Eggholder function Source: https://en.wikipedia.org/wiki/File:Eggholder_function.pdf. Image by Gaortizg. Licensed under Creative Commons CC BY-SA 3.0: https://creativecommons.org/licenses/by-sa/3.0/deed.en Explore more here: https://www.sfu.ca/~ssurjano/egg.htmlhttps://www.sfu.ca/~ssurjano/egg.html#
The eggholder function is a mathematical function often used as a benchmark problem for optimization algorithms. It’s designed to be challenging due to its complex landscape with multiple local minima and one global minimum. The function is defined as:
The function has a global minimum at ( f(512, 404.2319) = -959.6407 ), which is surrounded by several local minima and maxima. The “eggholder” name comes from the visual appearance of the function’s plot, which somewhat resembles an egg holder.
Imagine you’re trying to find the lowest point on a hilly landscape, but there are many hills and valleys, and you can’t see the whole picture at once. The eggholder function is like a mathematical version of this situation. It’s used to test how well different methods, like optimization algorithms, can find the lowest point (the global minimum) in a complicated landscape with lots of ups and downs.
In high school, you might have learned about functions and how to find their minimum or maximum points. The eggholder function is special because it’s quite tricky. It has many peaks and valleys, and finding the lowest point isn’t easy. So, mathematicians and computer scientists use it to test new methods or algorithms for finding the best solution in complex situations.
1.10.2. Real Coded Operators#
1.10.2.1. Blend Crossover#
Blend Crossover. (BLX)
he α value is commonly set to 0.5, resulting in a selection interval twice as wide
as the interval between the parents.
1.10.2.2. Simulated Binary Crossover#
Simulated Binary Crossover. (SLX)
The value of β, also known as the spread factor, is calculated using a combination of a randomly chosen value and a pre-determined parameter known as η (eta), distribution index, or crowding factor. With larger values of η, offspring will tend to be more similar to their parents. Common values of η are between 10 and 20.
1.10.2.3. Normally Distributed (or Gaussian) Mutation#
Original Value is placed with a random number generated using normal distribution wit predetermined values for mean and standard deviation.
1.10.2.4. cxSimulatedBinaryBounded#
is a bounded version of cxSimulateBinary() operator, accepting the arguments low and up as the lower and upper boundaries of the search space, respectively
1.10.3. TASK: Using DEAP to calculate individual fitness using Eggholder#
When calling the implementation:
# create initial population (generation 0):
population = toolbox.populationCreator(n=POPULATION_SIZE)
# prepare the statistics object:
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("min", np.min)
stats.register("avg", np.mean)
# define the hall-of-fame object:
hof = tools.HallOfFame(HALL_OF_FAME_SIZE)
# perform the Genetic Algorithm flow with elitism:
population, logbook = elitism.eaSimpleWithElitism(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION,
ngen=MAX_GENERATIONS, stats=stats, halloffame=hof, verbose=True)
# print info for best solution found:
best = hof.items[0]
print("-- Best Individual = ", best)
print("-- Best Fitness = ", best.fitness.values[0])
# extract statistics:
minFitnessValues, meanFitnessValues = logbook.select("min", "avg")
# plot statistics:
sns.set_style("whitegrid")
plt.plot(minFitnessValues, color='red')
plt.plot(meanFitnessValues, color='green')
plt.xlabel('Generation')
plt.ylabel('Min / Average Fitness')
plt.title('Min and Average fitness over Generations')
plt.show()
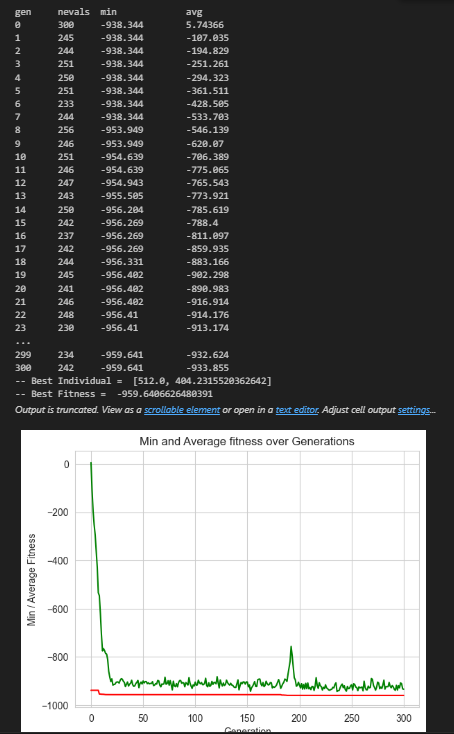
Fig. 1.6 Expected Output.#
Complete the following template:
from deap import base
from deap import creator
from deap import tools
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import elitism
# problem constants:
DIMENSIONS = 2 # number of dimensions
BOUND_LOW, BOUND_UP = -512.0, 512.0 # boundaries for all dimensions
# Genetic Algorithm constants:
POPULATION_SIZE = 300
P_CROSSOVER = 0.9 # probability for crossover
P_MUTATION = 0.1 # (try also 0.5) probability for mutating an individual
MAX_GENERATIONS = 300
HALL_OF_FAME_SIZE = 30
CROWDING_FACTOR = 20.0 # crowding factor for crossover and mutation
# set the random seed:
RANDOM_SEED = 42
random.seed(RANDOM_SEED)
toolbox = base.Toolbox()
# TODO define a single objective, minimizing fitness strategy:
# TODO create the Individual class based on list:
# helper function for creating random real numbers uniformly distributed within a given range [low, up]
# it assumes that the range is the same for every dimension
def randomFloat(low, up):
return [random.uniform(l, u) for l, u in zip([low] * DIMENSIONS, [up] * DIMENSIONS)]
# TODO create an operator that randomly returns a float in the desired range and dimension:
# TODO create the individual operator to fill up an Individual instance:
# TODO create the population operator to generate a list of individuals:
# TDOO Complete Eggholder function as the given individual's fitness:
def eggholder(individual):
x = individual[0]
y = individual[1]
# TODO implement the Eggholder function: f(x, y) = (- (y + 47) * sin(sqrt(abs(x/2 + (y + 47)))) - x * sin(sqrt(abs(x - (y + 47))))
return f, # return a tuple
toolbox.register("evaluate", eggholder)
# genetic operators:
toolbox.register("select", tools.selTournament, tournsize=2)
"""
Given that the selection operator is independent5.
of the individual type, and we've had a good experience so far using the
tournament selection with a tournament size of 2, coupled with the elitist
approach, we'll continue to use it here. The crossover and mutation operators, on
the other hand, need to be specialized for floating-point numbers within given
boundaries, and therefore we use the DEAP-provided
cxSimulatedBinaryBounded operator for crossover, and
the mutPolynomialBounded operator for mutation:
"""
# TODO register the crossover operator: using 'mate' as tools.cxSimulatedBinaryBounded and the crowding factor as CROWDING_FACTOR
# TODO register the mutation operator: using 'mutate' as tools.mutPolynomialBounded and the crowding factor as CROWDING_FACTOR
from deap import base
from deap import creator
from deap import tools
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import elitism
# problem constants:
DIMENSIONS = 2 # number of dimensions
BOUND_LOW, BOUND_UP = -512.0, 512.0 # boundaries for all dimensions
# Genetic Algorithm constants:
POPULATION_SIZE = 300
P_CROSSOVER = 0.9 # probability for crossover
P_MUTATION = 0.1 # (try also 0.5) probability for mutating an individual
MAX_GENERATIONS = 300
HALL_OF_FAME_SIZE = 30
CROWDING_FACTOR = 20.0 # crowding factor for crossover and mutation
# set the random seed:
RANDOM_SEED = 42
random.seed(RANDOM_SEED)
toolbox = base.Toolbox()
# define a single objective, minimizing fitness strategy:
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
# create the Individual class based on list:
creator.create("Individual", list, fitness=creator.FitnessMin)
# helper function for creating random real numbers uniformly distributed within a given range [low, up]
# it assumes that the range is the same for every dimension
def randomFloat(low, up):
return [random.uniform(l, u) for l, u in zip([low] * DIMENSIONS, [up] * DIMENSIONS)]
# create an operator that randomly returns a float in the desired range and dimension:
toolbox.register("attrFloat", randomFloat, BOUND_LOW, BOUND_UP)
# create the individual operator to fill up an Individual instance:
toolbox.register("individualCreator", tools.initIterate, creator.Individual, toolbox.attrFloat)
# create the population operator to generate a list of individuals:
toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator)
# Eggholder function as the given individual's fitness:
def eggholder(individual):
x = individual[0]
y = individual[1]
f = (-(y + 47.0) * np.sin(np.sqrt(abs(x/2.0 + (y + 47.0)))) - x * np.sin(np.sqrt(abs(x - (y + 47.0)))))
return f, # return a tuple
toolbox.register("evaluate", eggholder)
# genetic operators:
toolbox.register("select", tools.selTournament, tournsize=2)
toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR)
toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR, indpb=1.0/DIMENSIONS)
# create initial population (generation 0):
population = toolbox.populationCreator(n=POPULATION_SIZE)
# prepare the statistics object:
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("min", np.min)
stats.register("avg", np.mean)
# define the hall-of-fame object:
hof = tools.HallOfFame(HALL_OF_FAME_SIZE)
# perform the Genetic Algorithm flow with elitism:
population, logbook = elitism.eaSimpleWithElitism(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION,
ngen=MAX_GENERATIONS, stats=stats, halloffame=hof, verbose=True)
# print info for best solution found:
best = hof.items[0]
print("-- Best Individual = ", best)
print("-- Best Fitness = ", best.fitness.values[0])
# extract statistics:
minFitnessValues, meanFitnessValues = logbook.select("min", "avg")
# plot statistics:
sns.set_style("whitegrid")
plt.plot(minFitnessValues, color='red')
plt.plot(meanFitnessValues, color='green')
plt.xlabel('Generation')
plt.ylabel('Min / Average Fitness')
plt.title('Min and Average fitness over Generations')
plt.show()
gen nevals min avg
0 300 -938.344 5.74366
1 245 -938.344 -107.035
2 244 -938.344 -194.829
3 251 -938.344 -251.261
4 250 -938.344 -294.323
5 251 -938.344 -361.511
6 233 -938.344 -428.505
7 244 -938.344 -533.703
8 256 -953.949 -546.139
9 246 -953.949 -620.07
10 251 -954.639 -706.389
11 246 -954.639 -775.065
12 247 -954.943 -765.543
13 243 -955.505 -773.921
14 250 -956.204 -785.619
15 242 -956.269 -788.4
16 237 -956.269 -811.097
17 242 -956.269 -859.935
18 244 -956.331 -883.166
19 245 -956.402 -902.298
20 241 -956.402 -890.983
21 246 -956.402 -916.914
22 248 -956.41 -914.176
23 230 -956.41 -913.174
24 258 -956.41 -905.963
25 240 -956.415 -903.579
26 253 -956.416 -904.171
27 247 -956.416 -908.573
28 262 -956.416 -896.797
29 249 -956.416 -890.515
30 249 -956.416 -892.158
31 248 -956.418 -900.733
32 241 -956.418 -905.919
33 251 -956.418 -923.118
34 254 -956.419 -913.551
35 243 -956.419 -903.915
36 254 -956.419 -920.719
37 244 -956.419 -913.107
38 246 -956.419 -909.078
39 237 -956.419 -896.549
40 249 -956.419 -915.218
41 244 -956.419 -922.198
42 242 -956.419 -920.011
43 242 -956.419 -910.241
44 256 -956.419 -904.912
45 250 -956.419 -897.528
46 250 -956.419 -927.587
47 243 -956.419 -910.139
48 254 -956.419 -904.402
49 256 -956.419 -912.471
50 244 -956.419 -899.757
51 243 -956.421 -907.919
52 235 -956.421 -902.346
53 252 -956.421 -902.17
54 247 -956.421 -911.081
55 228 -956.421 -907.036
56 243 -956.421 -911.801
57 249 -956.421 -909.967
58 232 -956.421 -910.203
59 254 -956.422 -902.523
60 248 -956.422 -918.906
61 246 -956.422 -917.013
62 242 -956.422 -910.31
63 240 -956.422 -912.768
64 251 -956.422 -897.512
65 249 -956.422 -899.223
66 255 -956.422 -916.923
67 241 -956.422 -924.08
68 254 -956.422 -912.092
69 246 -956.422 -913.548
70 255 -956.422 -911.423
71 248 -956.422 -884.076
72 248 -956.422 -913.138
73 246 -956.422 -910.744
74 252 -956.423 -898.459
75 245 -956.423 -917.205
76 247 -956.423 -898.008
77 248 -956.423 -916.493
78 250 -956.423 -936.691
79 250 -956.423 -900.525
80 250 -956.423 -920.197
81 244 -956.423 -923.536
82 253 -956.423 -910.414
83 259 -956.423 -924.097
84 246 -956.423 -906.337
85 256 -956.424 -898.217
86 250 -956.424 -897.675
87 244 -956.424 -909.308
88 255 -956.424 -906.221
89 234 -956.424 -908.244
90 254 -956.424 -923.972
91 249 -956.424 -906.336
92 257 -956.424 -911.165
93 251 -956.424 -916.505
94 244 -956.424 -885.511
95 233 -956.424 -908.822
96 246 -956.424 -920.647
97 249 -956.424 -930.739
98 252 -956.424 -915.898
99 235 -956.424 -920.517
100 251 -956.424 -904.436
101 241 -956.424 -917.366
102 256 -956.424 -915.778
103 246 -956.424 -896.39
104 254 -956.424 -907.495
105 240 -956.424 -911.764
106 252 -956.424 -906.007
107 254 -956.424 -915.019
108 232 -956.424 -914.954
109 256 -956.424 -908.935
110 235 -956.424 -888.409
111 239 -956.424 -919.367
112 262 -956.424 -923.914
113 250 -956.424 -907.117
114 233 -956.424 -922.384
115 249 -956.424 -917.331
116 243 -956.424 -901.383
117 245 -956.424 -913.967
118 247 -956.424 -905.714
119 243 -956.424 -906.011
120 256 -956.424 -911.673
121 247 -956.424 -882.289
122 238 -956.424 -907.098
123 233 -956.424 -928.467
124 237 -956.424 -895.269
125 250 -956.424 -910.376
126 246 -956.424 -920.847
127 232 -956.424 -908.048
128 229 -956.424 -918.347
129 239 -956.424 -914.269
130 234 -956.424 -896.169
131 246 -956.424 -906.654
132 244 -956.424 -912.741
133 247 -956.424 -916.772
134 240 -956.424 -909.066
135 240 -956.424 -916.434
136 250 -956.424 -917.727
137 242 -956.424 -924.111
138 251 -956.424 -926.445
139 241 -956.424 -926.225
140 244 -956.424 -910.779
141 239 -956.424 -895.076
142 249 -956.424 -936.617
143 243 -956.424 -918.654
144 246 -956.424 -905.852
145 241 -956.424 -911.301
146 253 -956.424 -903.52
147 238 -956.424 -904.164
148 251 -956.424 -912.806
149 250 -956.424 -903.45
150 253 -956.424 -904.088
151 239 -956.424 -924.06
152 249 -956.424 -916.081
153 243 -956.424 -942.513
154 248 -956.424 -932.63
155 246 -956.424 -917.954
156 244 -956.424 -922.958
157 246 -956.424 -896.53
158 234 -956.424 -926.204
159 239 -956.424 -924.613
160 245 -956.424 -901.713
161 245 -956.424 -922.182
162 255 -956.426 -892.473
163 242 -956.426 -912.645
164 238 -956.426 -918.48
165 248 -956.427 -911.584
166 239 -956.427 -916.627
167 250 -956.428 -905.225
168 247 -956.428 -928.306
169 232 -956.428 -918.574
170 244 -956.428 -906.343
171 241 -956.428 -911.253
172 249 -956.428 -915.307
173 253 -956.428 -896.207
174 246 -956.428 -915.972
175 238 -956.428 -902.406
176 239 -956.428 -928.118
177 250 -956.428 -914.629
178 249 -956.428 -913.461
179 253 -956.428 -907.954
180 248 -956.428 -905.022
181 253 -956.428 -910.216
182 231 -956.428 -911.189
183 243 -956.43 -911.191
184 242 -956.43 -925.442
185 244 -956.431 -921.63
186 245 -956.432 -891.744
187 258 -956.432 -935.833
188 260 -956.433 -903.166
189 250 -956.433 -886.175
190 224 -956.434 -913.754
191 240 -956.434 -924.412
192 231 -956.436 -915.58
193 239 -956.436 -903.564
194 249 -956.436 -919.602
195 256 -956.436 -910.832
196 241 -956.436 -911.517
197 254 -956.436 -897.949
198 245 -956.436 -920.07
199 254 -956.436 -912.692
200 239 -956.436 -917.938
201 251 -956.437 -922.538
202 231 -956.437 -924.769
203 250 -956.437 -937.061
204 243 -956.437 -913.575
205 251 -956.437 -897.464
206 245 -956.437 -907.549
207 243 -956.438 -893.863
208 248 -956.438 -910.494
209 244 -956.438 -929.546
210 243 -956.438 -921.691
211 244 -956.438 -915.993
212 246 -956.438 -900.64
213 245 -956.438 -922.004
214 245 -956.438 -917.053
215 244 -956.438 -914.101
216 232 -956.438 -899.716
217 251 -956.438 -912.403
218 241 -956.438 -912.709
219 247 -956.438 -907.405
220 257 -956.438 -875.374
221 243 -956.438 -891.936
222 250 -956.438 -916.659
223 221 -956.438 -918.934
224 244 -956.438 -926.057
225 245 -956.438 -911.212
226 248 -956.438 -922.454
227 237 -956.438 -900.819
228 231 -956.438 -907.826
229 243 -956.438 -918.015
230 252 -956.438 -913.237
231 237 -956.438 -878.731
232 251 -956.438 -900.097
233 248 -956.438 -900.924
234 254 -956.438 -924.308
235 245 -956.438 -906.918
236 245 -956.438 -923.083
237 251 -956.438 -921.034
238 238 -956.438 -913.661
239 246 -956.438 -905.738
240 245 -956.438 -929.993
241 253 -956.438 -919.128
242 256 -956.439 -915.749
243 249 -956.439 -909.29
244 243 -956.439 -909.373
245 235 -956.439 -916.971
246 233 -956.439 -900.165
247 243 -956.457 -912.683
248 243 -956.457 -919.149
249 250 -956.457 -909.71
250 241 -956.457 -910.937
251 245 -956.457 -904.929
252 248 -956.457 -919.619
253 247 -956.457 -912.736
254 234 -956.457 -918.784
255 244 -956.459 -925.623
256 237 -956.459 -919.741
257 236 -956.459 -910.309
258 248 -956.461 -921.644
259 248 -956.461 -910.286
260 242 -956.462 -909.81
261 236 -956.462 -911.066
262 243 -956.462 -916.376
263 245 -956.462 -902.628
264 247 -956.462 -913.946
265 243 -956.462 -929.052
266 245 -956.462 -906.68
267 251 -956.462 -914.606
268 246 -956.462 -919.04
269 246 -956.462 -915.43
270 248 -956.462 -912.863
271 252 -956.464 -918.89
272 241 -956.464 -910.356
273 248 -956.464 -908.291
274 244 -956.464 -907.585
275 242 -956.464 -913.868
276 251 -956.464 -917.028
277 236 -956.464 -910.128
278 245 -956.464 -923.969
279 244 -956.464 -921.06
280 250 -956.464 -921.351
281 253 -956.464 -904.838
282 248 -956.464 -931.469
283 244 -956.464 -904.758
284 253 -956.464 -918.484
285 253 -956.464 -899.707
286 249 -956.464 -913.501
287 242 -956.464 -908.205
288 248 -956.464 -938.159
289 249 -956.464 -918.186
290 246 -956.464 -882.741
291 251 -956.464 -926.314
292 244 -956.464 -905.242
293 245 -956.464 -888.759
294 249 -956.464 -917.127
295 243 -956.464 -904.123
296 243 -956.464 -905.527
297 250 -956.464 -924.859
298 244 -956.464 -913.924
299 242 -956.464 -918.374
300 245 -956.464 -904.471
-- Best Individual = [483.909780775573, 434.4287397072944]
-- Best Fitness = -956.4641087935356
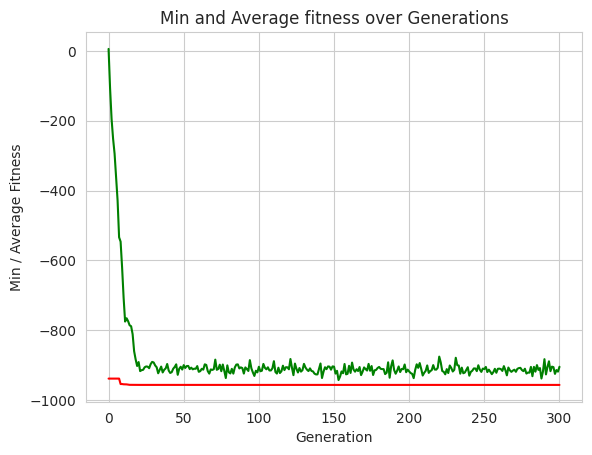
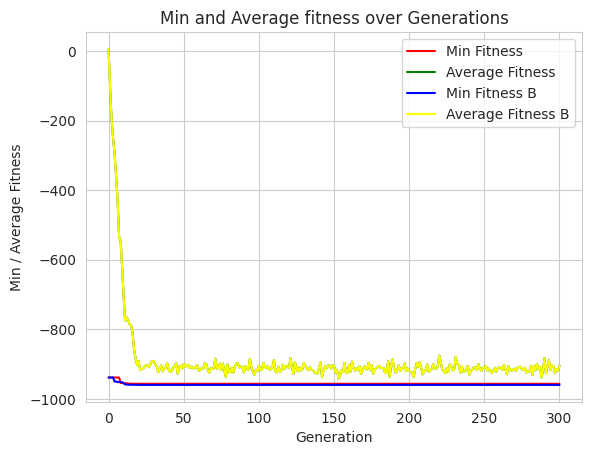
1.10.4. TASK Replot with 0.5 Mutation and show on the same plot#
from deap import base
from deap import creator
from deap import tools
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import elitism
# problem constants:
DIMENSIONS = 2 # number of dimensions
BOUND_LOW, BOUND_UP = -512.0, 512.0 # boundaries for all dimensions
# Genetic Algorithm constants:
POPULATION_SIZE = 300
P_CROSSOVER = 0.9 # probability for crossover
P_MUTATION = 0.5 # (try also 0.5) probability for mutating an individual
MAX_GENERATIONS = 300
HALL_OF_FAME_SIZE = 30
CROWDING_FACTOR = 20.0 # crowding factor for crossover and mutation
# set the random seed:
RANDOM_SEED = 42
random.seed(RANDOM_SEED)
toolbox = base.Toolbox()
# define a single objective, minimizing fitness strategy:
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
# create the Individual class based on list:
creator.create("Individual", list, fitness=creator.FitnessMin)
# helper function for creating random real numbers uniformly distributed within a given range [low, up]
# it assumes that the range is the same for every dimension
def randomFloat(low, up):
return [random.uniform(l, u) for l, u in zip([low] * DIMENSIONS, [up] * DIMENSIONS)]
# create an operator that randomly returns a float in the desired range and dimension:
toolbox.register("attrFloat", randomFloat, BOUND_LOW, BOUND_UP)
# create the individual operator to fill up an Individual instance:
toolbox.register("individualCreator", tools.initIterate, creator.Individual, toolbox.attrFloat)
# create the population operator to generate a list of individuals:
toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator)
# Eggholder function as the given individual's fitness:
def eggholder(individual):
x = individual[0]
y = individual[1]
f = (-(y + 47.0) * np.sin(np.sqrt(abs(x/2.0 + (y + 47.0)))) - x * np.sin(np.sqrt(abs(x - (y + 47.0)))))
return f, # return a tuple
toolbox.register("evaluate", eggholder)
# genetic operators:
toolbox.register("select", tools.selTournament, tournsize=2)
toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR)
toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=CROWDING_FACTOR, indpb=1.0/DIMENSIONS)
# TODO Show in sam eplot but as blue and yellow lines instead. with the previous plot
# create initial population (generation 0):
population_b = toolbox.populationCreator(n=POPULATION_SIZE)
# prepare the statistics object:
stats_b = tools.Statistics(lambda ind: ind.fitness.values)
stats_b.register("min", np.min)
stats_b.register("avg", np.mean)
# define the hall-of-fame object:
hof = tools.HallOfFame(HALL_OF_FAME_SIZE)
# perform the Genetic Algorithm flow with elitism:
population_b, logbook_b = elitism.eaSimpleWithElitism(population_b, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION,
ngen=MAX_GENERATIONS, stats=stats_b, halloffame=hof, verbose=True)
# print info for best solution found:
best = hof.items[0]
print("-- Best Individual = ", best)
print("-- Best Fitness = ", best.fitness.values[0])
# extract statistics:
minFitnessValues_b, meanFitnessValues_b = logbook_b.select("min", "avg")
# plot statistics:
sns.set_style("whitegrid")
plt.plot(minFitnessValues, color='red')
plt.plot(meanFitnessValues, color='green')
plt.plot(minFitnessValues_b, color='blue')
plt.plot(meanFitnessValues, color='yellow')
plt.xlabel('Generation')
plt.ylabel('Min / Average Fitness')
# Add legends.
plt.legend(['Min Fitness', 'Average Fitness', 'Min Fitness B', 'Average Fitness B'])
plt.title('Min and Average fitness over Generations')
plt.show()
gen nevals min avg
0 300 -938.344 5.74366
1 256 -938.344 -93.6859
2 261 -938.344 -199.776
3 260 -938.344 -242.383
4 257 -949.799 -277.752
5 255 -949.799 -340.727
6 255 -951.464 -401.777
7 258 -951.464 -458.552
8 254 -951.464 -464.904
9 258 -952.016 -540.356
10 249 -954.245 -569.033
11 254 -958.514 -548.672
12 261 -958.514 -577.511
13 254 -959.024 -578.77
14 248 -959.024 -595.563
15 261 -959.285 -587.904
16 256 -959.304 -618.27
17 259 -959.377 -596.288
18 256 -959.485 -638.201
19 262 -959.508 -670.193
20 253 -959.557 -705.507
21 260 -959.575 -702.257
22 256 -959.606 -716.336
23 264 -959.636 -715.322
24 256 -959.636 -771.18
25 263 -959.636 -763.546
26 262 -959.638 -739.197
27 255 -959.638 -751.84
28 265 -959.638 -795.878
29 256 -959.638 -752.338
30 256 -959.639 -757.67
31 251 -959.64 -762.326
32 252 -959.64 -734.005
33 258 -959.64 -758.626
34 250 -959.64 -731.062
35 250 -959.64 -717.838
36 251 -959.64 -745.382
37 259 -959.641 -753.785
38 255 -959.641 -741.456
39 261 -959.641 -721.202
40 262 -959.641 -739.42
41 259 -959.641 -780.229
42 255 -959.641 -734.662
43 250 -959.641 -747.223
44 255 -959.641 -756.578
45 257 -959.641 -720.683
46 254 -959.641 -794.43
47 254 -959.641 -753.234
48 250 -959.641 -745.042
49 261 -959.641 -726.402
50 261 -959.641 -736.484
51 263 -959.641 -714.715
52 255 -959.641 -751.426
53 255 -959.641 -762.815
54 254 -959.641 -766.396
55 260 -959.641 -738.426
56 263 -959.641 -752.669
57 256 -959.641 -745.656
58 262 -959.641 -777.061
59 254 -959.641 -750.837
60 254 -959.641 -752.566
61 266 -959.641 -765.31
62 252 -959.641 -738.543
63 264 -959.641 -728.439
64 263 -959.641 -742.71
65 262 -959.641 -725.614
66 260 -959.641 -714.957
67 258 -959.641 -699.017
68 255 -959.641 -762.248
69 259 -959.641 -753.336
70 258 -959.641 -724.914
71 259 -959.641 -756.512
72 258 -959.641 -746.023
73 247 -959.641 -797.67
74 252 -959.641 -789.766
75 262 -959.641 -776.967
76 257 -959.641 -780.892
77 257 -959.641 -760.575
78 257 -959.641 -744.508
79 261 -959.641 -766.537
80 260 -959.641 -758.173
81 255 -959.641 -737.503
82 257 -959.641 -740.326
83 258 -959.641 -775.877
84 257 -959.641 -751.299
85 258 -959.641 -749.458
86 256 -959.641 -720.814
87 254 -959.641 -709.52
88 255 -959.641 -686.135
89 258 -959.641 -738.067
90 243 -959.641 -774.626
91 258 -959.641 -755.753
92 257 -959.641 -741.26
93 255 -959.641 -760.156
94 254 -959.641 -708.15
95 252 -959.641 -744.25
96 252 -959.641 -767.987
97 254 -959.641 -776.67
98 252 -959.641 -785.319
99 263 -959.641 -755.387
100 258 -959.641 -737.3
101 254 -959.641 -746.734
102 253 -959.641 -727.907
103 248 -959.641 -733.329
104 246 -959.641 -724.901
105 259 -959.641 -758.727
106 256 -959.641 -749.133
107 250 -959.641 -763.872
108 253 -959.641 -737.578
109 260 -959.641 -715.57
110 259 -959.641 -749.636
111 259 -959.641 -750.613
112 262 -959.641 -744.497
113 267 -959.641 -730.266
114 259 -959.641 -800.164
115 258 -959.641 -784.857
116 247 -959.641 -742.412
117 261 -959.641 -794.012
118 262 -959.641 -768.131
119 257 -959.641 -772.022
120 259 -959.641 -730.852
121 245 -959.641 -739.778
122 258 -959.641 -740.574
123 256 -959.641 -701.608
124 257 -959.641 -755.13
125 255 -959.641 -759.577
126 255 -959.641 -804.498
127 262 -959.641 -739.028
128 257 -959.641 -763.068
129 262 -959.641 -744.232
130 258 -959.641 -748.839
131 260 -959.641 -764.929
132 244 -959.641 -783.832
133 262 -959.641 -732.722
134 253 -959.641 -733.872
135 253 -959.641 -719.554
136 250 -959.641 -748.439
137 256 -959.641 -766.022
138 249 -959.641 -759.738
139 253 -959.641 -763.703
140 254 -959.641 -726.936
141 257 -959.641 -709.665
142 256 -959.641 -736.185
143 260 -959.641 -762.962
144 246 -959.641 -789.74
145 245 -959.641 -731.139
146 258 -959.641 -742.358
147 252 -959.641 -779.884
148 257 -959.641 -752.867
149 260 -959.641 -752.175
150 255 -959.641 -725.182
151 263 -959.641 -777.36
152 263 -959.641 -770.311
153 261 -959.641 -762.673
154 256 -959.641 -746.876
155 257 -959.641 -739.719
156 259 -959.641 -744.049
157 263 -959.641 -751.625
158 258 -959.641 -768.99
159 261 -959.641 -723.516
160 262 -959.641 -713.253
161 263 -959.641 -748.435
162 259 -959.641 -748.054
163 255 -959.641 -773.437
164 258 -959.641 -746.575
165 258 -959.641 -737.424
166 262 -959.641 -769.593
167 256 -959.641 -735.236
168 253 -959.641 -721.385
169 251 -959.641 -761.908
170 254 -959.641 -789.053
171 264 -959.641 -755.806
172 248 -959.641 -730.442
173 255 -959.641 -750.957
174 258 -959.641 -780.144
175 257 -959.641 -755.878
176 255 -959.641 -766.571
177 261 -959.641 -743.843
178 254 -959.641 -747.481
179 257 -959.641 -742.401
180 262 -959.641 -739.047
181 258 -959.641 -697.684
182 263 -959.641 -797.708
183 263 -959.641 -769.063
184 259 -959.641 -738.333
185 255 -959.641 -753.46
186 261 -959.641 -745.397
187 241 -959.641 -729.586
188 252 -959.641 -756.608
189 258 -959.641 -723.37
190 254 -959.641 -724.19
191 260 -959.641 -763.635
192 260 -959.641 -769.969
193 257 -959.641 -748.303
194 251 -959.641 -751.2
195 261 -959.641 -725.999
196 256 -959.641 -755.321
197 254 -959.641 -747.918
198 256 -959.641 -718.149
199 253 -959.641 -745.203
200 250 -959.641 -747.445
201 260 -959.641 -779.561
202 258 -959.641 -776.306
203 248 -959.641 -753.287
204 261 -959.641 -752.361
205 254 -959.641 -733.352
206 253 -959.641 -741.351
207 251 -959.641 -726.527
208 253 -959.641 -729.826
209 254 -959.641 -733.898
210 250 -959.641 -750.296
211 257 -959.641 -758.197
212 260 -959.641 -777.239
213 259 -959.641 -685.463
214 257 -959.641 -716.25
215 257 -959.641 -721.161
216 251 -959.641 -763.303
217 250 -959.641 -777.05
218 261 -959.641 -755.264
219 249 -959.641 -763.745
220 250 -959.641 -753.404
221 257 -959.641 -753.239
222 260 -959.641 -734.601
223 257 -959.641 -734.809
224 249 -959.641 -740.223
225 252 -959.641 -731.885
226 246 -959.641 -768.486
227 248 -959.641 -732.126
228 254 -959.641 -748.677
229 267 -959.641 -756.971
230 259 -959.641 -710.17
231 257 -959.641 -752.838
232 254 -959.641 -746.258
233 262 -959.641 -732.468
234 257 -959.641 -721.263
235 253 -959.641 -747.722
236 261 -959.641 -770.98
237 260 -959.641 -757.523
238 256 -959.641 -728.39
239 252 -959.641 -771.427
240 259 -959.641 -755.311
241 260 -959.641 -757.264
242 262 -959.641 -780.184
243 259 -959.641 -733.485
244 261 -959.641 -735.899
245 256 -959.641 -730.978
246 258 -959.641 -787.235
247 254 -959.641 -754.902
248 257 -959.641 -770.294
249 266 -959.641 -772.589
250 257 -959.641 -754.046
251 254 -959.641 -727.615
252 263 -959.641 -753.933
253 256 -959.641 -766.426
254 253 -959.641 -734.06
255 252 -959.641 -732.101
256 248 -959.641 -787.523
257 257 -959.641 -759.938
258 260 -959.641 -767.575
259 257 -959.641 -729.381
260 257 -959.641 -722.87
261 249 -959.641 -783.715
262 246 -959.641 -755.976
263 263 -959.641 -752.765
264 258 -959.641 -760.53
265 258 -959.641 -725.087
266 246 -959.641 -749.353
267 259 -959.641 -748.779
268 257 -959.641 -687.252
269 254 -959.641 -705.406
270 248 -959.641 -761.802
271 252 -959.641 -753.18
272 259 -959.641 -773.835
273 262 -959.641 -722.396
274 258 -959.641 -747.301
275 260 -959.641 -732.403
276 256 -959.641 -763.088
277 250 -959.641 -749.093
278 250 -959.641 -757.96
279 247 -959.641 -766.822
280 253 -959.641 -767.009
281 258 -959.641 -738.958
282 257 -959.641 -769.827
283 256 -959.641 -777.053
284 254 -959.641 -756.768
285 260 -959.641 -736.25
286 254 -959.641 -755.565
287 257 -959.641 -774.093
288 255 -959.641 -744.925
289 247 -959.641 -789.205
290 259 -959.641 -746.968
291 251 -959.641 -710.721
292 250 -959.641 -715.619
293 252 -959.641 -704.073
294 259 -959.641 -707.549
295 249 -959.641 -750.2
296 252 -959.641 -764.914
297 254 -959.641 -777.263
298 257 -959.641 -774.444
299 257 -959.641 -780.336
300 256 -959.641 -778.702
-- Best Individual = [512.0, 404.2318049696766]
-- Best Fitness = -959.640662720851