1.6. Solving the N Queens Problem#
1.6.1. Problem Description.#
Originally known as the eight-queen puzzle, the classic N-Queens problem originated from the game of chess, and the 8x8 chessboard was its early playground. The task was to place eight chess queens on the board without any two of them threatening each other. In other words, no two queens can share the same row, same column, or same diagonal. The N-Queens problem is similar, using an N×N chessboard and N chess queens
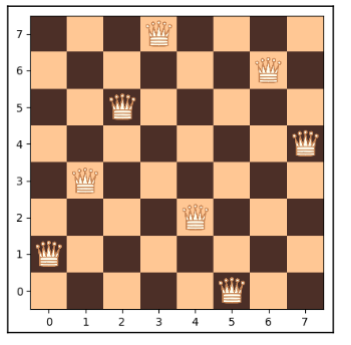
Fig. 1.3 One of the 92 possible solutions to the 8-queens problem#
1.6.1.1. 1. Explain why to select this count of population.#
Why is this basically selecting for
offspring = toolbox.select(population, len(population) - hof_size)?
1.7. So it replaces with the selected into that count?#
[ ] Does The individual have a fitness value?
The first individual created will be a simple list containing floats. In order to produce this kind of individual, we need to create an Individual class, using the creator, that will inherit from the standard list type and have a fitness attribute.
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
(3.0,),
(6.0,),
(7.0,),
(4.0,),
(6.0,),
(5.0,),
(6.0,),
(7.0,),
(7.0,),
(7.0,),
(8.0,),
(4.0,),
(8.0,),
(7.0,),
(9.0,),
(6.0,)
[ ] How does Torunament Select work?
Not even ranking the proper value there?
Gosh you should have just checked the code:
def selTournament(individuals, k, tournsize, fit_attr="fitness"):
"""Select the best individual among *tournsize* randomly chosen
individuals, *k* times. The list returned contains
references to the input *individuals*.
:param individuals: A list of individuals to select from.
:param k: The number of individuals to select.
:param tournsize: The number of individuals participating in each tournament.
:param fit_attr: The attribute of individuals to use as selection criterion
:returns: A list of selected individuals.
This function uses the :func:`~random.choice` function from the python base
:mod:`random` module.
"""
chosen = []
for i in range(k):
aspirants = selRandom(individuals, tournsize)
chosen.append(max(aspirants, key=attrgetter(fit_attr)))
return chosen
def selRandom(individuals, k):
"""Select *k* individuals at random from the input *individuals* with
replacement. The list returned contains references to the input
*individuals*.
:param individuals: A list of individuals to select from.
:param k: The number of individuals to select.
:returns: A list of selected individuals.
This function uses the :func:`~random.choice` function from the
python base :mod:`random` module.
"""
return [random.choice(individuals) for i in range(k)]
Why is it still okay to use tornament selection on this case?
Compare it with the following:
def eaSimple(population, toolbox, cxpb, mutpb, ngen, stats=None,
halloffame=None, verbose=__debug__):
"""This algorithm reproduce the simplest evolutionary algorithm as
presented in chapter 7 of [Back2000]_.
:param population: A list of individuals.
:param toolbox: A :class:`~deap.base.Toolbox` that contains the evolution
operators.
:param cxpb: The probability of mating two individuals.
:param mutpb: The probability of mutating an individual.
:param ngen: The number of generation.
:param stats: A :class:`~deap.tools.Statistics` object that is updated
inplace, optional.
:param halloffame: A :class:`~deap.tools.HallOfFame` object that will
contain the best individuals, optional.
:param verbose: Whether or not to log the statistics.
:returns: The final population
:returns: A class:`~deap.tools.Logbook` with the statistics of the
evolution
The algorithm takes in a population and evolves it in place using the
:meth:`varAnd` method. It returns the optimized population and a
:class:`~deap.tools.Logbook` with the statistics of the evolution. The
logbook will contain the generation number, the number of evaluations for
each generation and the statistics if a :class:`~deap.tools.Statistics` is
given as argument. The *cxpb* and *mutpb* arguments are passed to the
:func:`varAnd` function. The pseudocode goes as follow ::
evaluate(population)
for g in range(ngen):
population = select(population, len(population))
offspring = varAnd(population, toolbox, cxpb, mutpb)
evaluate(offspring)
population = offspring
As stated in the pseudocode above, the algorithm goes as follow. First, it
evaluates the individuals with an invalid fitness. Second, it enters the
generational loop where the selection procedure is applied to entirely
replace the parental population. The 1:1 replacement ratio of this
algorithm **requires** the selection procedure to be stochastic and to
select multiple times the same individual, for example,
:func:`~deap.tools.selTournament` and :func:`~deap.tools.selRoulette`.
Third, it applies the :func:`varAnd` function to produce the next
generation population. Fourth, it evaluates the new individuals and
compute the statistics on this population. Finally, when *ngen*
generations are done, the algorithm returns a tuple with the final
population and a :class:`~deap.tools.Logbook` of the evolution.
.. note::
Using a non-stochastic selection method will result in no selection as
the operator selects *n* individuals from a pool of *n*.
This function expects the :meth:`toolbox.mate`, :meth:`toolbox.mutate`,
:meth:`toolbox.select` and :meth:`toolbox.evaluate` aliases to be
registered in the toolbox.
.. [Back2000] Back, Fogel and Michalewicz, "Evolutionary Computation 1 :
Basic Algorithms and Operators", 2000.
"""
logbook = tools.Logbook()
logbook.header = ['gen', 'nevals'] + (stats.fields if stats else [])
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in population if not ind.fitness.valid]
fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
if halloffame is not None:
halloffame.update(population)
record = stats.compile(population) if stats else {}
logbook.record(gen=0, nevals=len(invalid_ind), **record)
if verbose:
print(logbook.stream)
# Begin the generational process
for gen in range(1, ngen + 1):
# Select the next generation individuals
offspring = toolbox.select(population, len(population))
# Vary the pool of individuals
offspring = varAnd(offspring, toolbox, cxpb, mutpb)
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
# Update the hall of fame with the generated individuals
if halloffame is not None:
halloffame.update(offspring)
# Replace the current population by the offspring
population[:] = offspring
# Append the current generation statistics to the logbook
record = stats.compile(population) if stats else {}
logbook.record(gen=gen, nevals=len(invalid_ind), **record)
if verbose:
print(logbook.stream)
return population, logbook
1.7.1. Create N Queens Problem.#
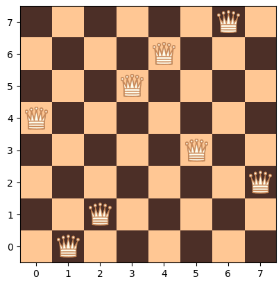
Create a NQueensProblme as when running:
# create a problem instance:
nQueens = NQueensProblem(8)
# a solution with 3 violations:
solution = [1, 2, 7, 5, 0, 3, 4, 6]
print("Number of violations = ", nQueens.getViolationsCount(solution))
plot = nQueens.plotBoard(solution)
plot.show()
It should show the following:
Complete the following base code.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
class NQueensProblem:
"""This class encapsulates the N-Queens problem
"""
def __init__(self, numOfQueens):
"""
:param numOfQueens: the number of queens in the problem
"""
# TODO initialize the number of queens
def __len__(self):
"""
:return: the number of queens
"""
# TODO return the number of queens
def getViolationsCount(self, positions):
"""
Calculates the number of violations in the given solution
Since the input contains unique indices of columns for each row, no row or column violations are possible,
Only the diagonal violations need to be counted.
:param positions: a list of indices corresponding to the positions of the queens in each row
:return: the calculated value
"""
if len(positions) != self.numOfQueens:
raise ValueError("size of positions list should be equal to ", self.numOfQueens)
violations = 0
# iterate over every pair of queens and find if they are on the same diagonal:
for i in range(len(positions)):
for j in range(i + 1, len(positions)):
# first queen in pair:
column1 = i
row1 = positions[i]
# second queen in pair:
column2 = j
row2 = positions[j]
# look for diagonal threat for th ecurrent pair:
if abs(column1 - column2) == abs(row1 - row2):
violations += 1
return violations
def plotBoard(self, positions):
"""
Plots the positions of the queens on the board according to the given solution
:param positions: a list of indices corresponding to the positions of the queens in each row.
"""
if len(positions) != self.numOfQueens:
raise ValueError("size of positions list should be equal to ", self.numOfQueens)
fig, ax = plt.subplots()
# start with the board's squares:
board = np.zeros((self.numOfQueens, self.numOfQueens))
# change color of every other square:
board[::2, 1::2] = 1
board[1::2, ::2] = 1
# draw the squares with two different colors:
# TODO Show th board as an alternating #ffc794 and #4c2f27 colors
# ax.imshow(board, interpolation='none', cmap=mpl.colors.ListedColormap(['#ffc794', '#4c2f27']))
# read the queen image thumbnail and give it a spread of 70% of the square dimensions:
queenThumbnail = plt.imread('queen-thumbnail.png')
thumbnailSpread = 0.70 * np.array([-1, 1, -1, 1]) / 2 # spread is [left, right, bottom, top]
# iterate over the queen positions - i is the row, j is the column:
for i, j in enumerate(positions):
# place the thumbnail on the matching square:
# TODO use the ax.imshow to place the queenThumbnail on the board
# ax.imshow(queenThumbnail, extent=[j, j, i, i] + thumbnailSpread)
# show the row and column indexes:
ax.set(xticks=list(range(self.numOfQueens)), yticks=list(range(self.numOfQueens)))
ax.axis('image') # scale the plot as square-shaped
return plt
1.7.1.1. Solution#
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
class NQueensProblem:
"""This class encapsulates the N-Queens problem
"""
def __init__(self, numOfQueens):
"""
:param numOfQueens: the number of queens in the problem
"""
self.numOfQueens = numOfQueens
def __len__(self):
"""
:return: the number of queens
"""
return self.numOfQueens
def getViolationsCount(self, positions):
"""
Calculates the number of violations in the given solution
Since the input contains unique indices of columns for each row, no row or column violations are possible,
Only the diagonal violations need to be counted.
:param positions: a list of indices corresponding to the positions of the queens in each row
:return: the calculated value
"""
if len(positions) != self.numOfQueens:
raise ValueError("size of positions list should be equal to ", self.numOfQueens)
violations = 0
# iterate over every pair of queens and find if they are on the same diagonal:
for i in range(len(positions)):
for j in range(i + 1, len(positions)):
# first queen in pair:
column1 = i
row1 = positions[i]
# second queen in pair:
column2 = j
row2 = positions[j]
# look for diagonal threat for th ecurrent pair:
if abs(column1 - column2) == abs(row1 - row2):
violations += 1
return violations
def plotBoard(self, positions):
"""
Plots the positions of the queens on the board according to the given solution
:param positions: a list of indices corresponding to the positions of the queens in each row.
"""
if len(positions) != self.numOfQueens:
raise ValueError("size of positions list should be equal to ", self.numOfQueens)
fig, ax = plt.subplots()
# start with the board's squares:
board = np.zeros((self.numOfQueens, self.numOfQueens))
# change color of every other square:
board[::2, 1::2] = 1
board[1::2, ::2] = 1
# draw the squares with two different colors:
ax.imshow(board, interpolation='none', cmap=mpl.colors.ListedColormap(['#ffc794', '#4c2f27']))
# read the queen image thumbnail and give it a spread of 70% of the square dimensions:
queenThumbnail = plt.imread('queen-thumbnail.png')
thumbnailSpread = 0.70 * np.array([-1, 1, -1, 1]) / 2 # spread is [left, right, bottom, top]
# iterate over the queen positions - i is the row, j is the column:
for i, j in enumerate(positions):
# place the thumbnail on the matching square:
ax.imshow(queenThumbnail, extent=[j, j, i, i] + thumbnailSpread)
# show the row and column indexes:
ax.set(xticks=list(range(self.numOfQueens)), yticks=list(range(self.numOfQueens)))
ax.axis('image') # scale the plot as square-shaped
return plt
# create a problem instance:
nQueens = NQueensProblem(8)
# a solution with 3 violations:
solution = [1, 2, 7, 5, 0, 3, 4, 6]
print("Number of violations = ", nQueens.getViolationsCount(solution))
plot = nQueens.plotBoard(solution)
plot.show()
Number of violations = 3
1.7.2. Solve the NQueens Problem using Genetic Algorithm#
As said above,find a way to solve it using the ste base NQueeens Problem.
[ ] Record the following on the
Logbook:
gen, nevals, min, avg
[ ] Plot the bet solution on the chessboard.
[ ] Show the improvement of the solution over the generations.
1.7.2.1. Solution#
from deap import base
from deap import creator
from deap import tools
import random
import array
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import elitism
# problem constants:
NUM_OF_QUEENS = 16
# Genetic Algorithm constants:
POPULATION_SIZE = 300
MAX_GENERATIONS = 100
HALL_OF_FAME_SIZE = 30
P_CROSSOVER = 0.9 # probability for crossover
P_MUTATION = 0.1 # probability for mutating an individual
# set the random seed for repeatable results
RANDOM_SEED = 42
random.seed(RANDOM_SEED)
# create the desired N-
nQueens = NQueensProblem(NUM_OF_QUEENS)
toolbox = base.Toolbox()
# define a single objective, minimizing fitness strategy:
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
# Why is the default weight -1.0? What does it mean? => This is the way to communicate to DEAP that the fitness is to be minimized. If you want to maximize the fitness, you should use 1.0.
# create the Individual class based on list of integers:
creator.create("Individual", array.array, typecode='i', fitness=creator.FitnessMin)
# create an operator that generates randomly shuffled indices:
toolbox.register("randomOrder", random.sample, range(len(nQueens)), len(nQueens))
# create the individual creation operator to fill up an Individual instance with shuffled indices:
toolbox.register("individualCreator", tools.initIterate, creator.Individual, toolbox.randomOrder)
# create the population creation operator to generate a list of individuals:
toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator)
# fitness calculation - compute the total distance of the list of cities represented by indices:
def getViolationsCount(individual):
return nQueens.getViolationsCount(individual), # return a tuple
toolbox.register("evaluate", getViolationsCount)
# Genetic operators:
toolbox.register("select", tools.selTournament, tournsize=2)
toolbox.register("mate", tools.cxUniformPartialyMatched, indpb=2.0/len(nQueens))
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=1.0/len(nQueens))
# create initial population (generation 0):
population = toolbox.populationCreator(n=POPULATION_SIZE)
# prepare the statistics object:
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("min", np.min)
stats.register("avg", np.mean)
# define the hall-of-fame object:
hof = tools.HallOfFame(HALL_OF_FAME_SIZE)
# perform the Genetic Algorithm flow with hof feature added:
population, logbook = elitism.eaSimpleWithElitism(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION,
ngen=MAX_GENERATIONS, stats=stats, halloffame=hof, verbose=True)
# Question? hy since the k is n size of the population. Why are we selecting tournament of size selection of n members?
# print hall of fame members info:
print("- Best solutions are:")
for i in range(HALL_OF_FAME_SIZE):
print(i, ": ", hof.items[i].fitness.values[0], " -> ", hof.items[i])
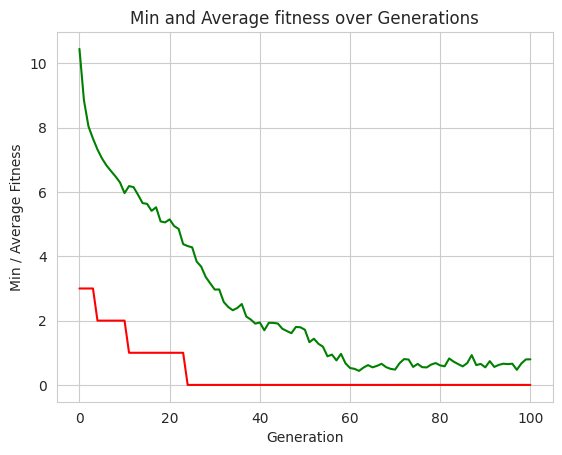
# plot statistics:
minFitnessValues, meanFitnessValues = logbook.select("min", "avg")
plt.figure(1)
sns.set_style("whitegrid")
plt.plot(minFitnessValues, color='red')
plt.plot(meanFitnessValues, color='green')
plt.xlabel('Generation')
plt.ylabel('Min / Average Fitness')
plt.title('Min and Average fitness over Generations')
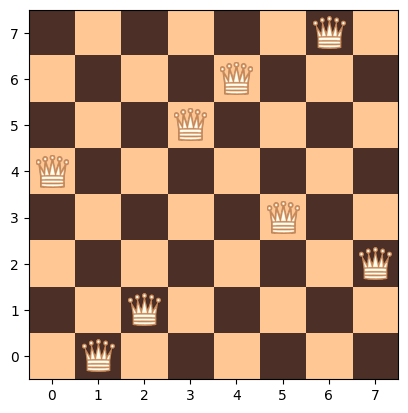
# plot best solution:
sns.set_style("whitegrid", {'axes.grid' : False})
nQueens.plotBoard(hof.items[0])
# show both plots:
plt.show()
gen nevals min avg
0 300 3 10.4533
1 246 3 8.85333
2 237 3 8.04333
3 239 3 7.66333
4 244 2 7.32333
5 244 2 7.04667
6 249 2 6.82667
7 241 2 6.65333
8 251 2 6.48667
9 251 2 6.29667
10 241 2 5.96667
11 255 1 6.18667
12 255 1 6.15333
13 256 1 5.91333
14 253 1 5.65667
15 239 1 5.63333
16 247 1 5.41667
17 247 1 5.52667
18 244 1 5.08667
19 249 1 5.05667
20 251 1 5.15
21 241 1 4.94333
22 240 1 4.85333
23 250 1 4.38
24 227 0 4.32
25 245 0 4.28
26 238 0 3.83667
27 252 0 3.68
28 242 0 3.36
29 242 0 3.16
30 245 0 2.96667
31 251 0 2.97
32 245 0 2.58
33 242 0 2.42333
34 246 0 2.32333
35 256 0 2.39333
36 251 0 2.51667
37 247 0 2.12667
38 248 0 2.03333
39 244 0 1.90667
40 251 0 1.94333
41 243 0 1.7
42 239 0 1.93333
43 234 0 1.93
44 246 0 1.91
45 241 0 1.74667
46 233 0 1.67667
47 242 0 1.61
48 240 0 1.80333
49 242 0 1.79333
50 254 0 1.71667
51 244 0 1.33
52 253 0 1.43667
53 244 0 1.28
54 248 0 1.19
55 235 0 0.89
56 249 0 0.943333
57 254 0 0.763333
58 248 0 0.966667
59 240 0 0.673333
60 242 0 0.526667
61 249 0 0.5
62 253 0 0.436667
63 237 0 0.54
64 243 0 0.616667
65 244 0 0.546667
66 244 0 0.593333
67 243 0 0.656667
68 258 0 0.553333
69 245 0 0.5
70 244 0 0.476667
71 241 0 0.676667
72 237 0 0.803333
73 253 0 0.79
74 241 0 0.56
75 255 0 0.653333
76 248 0 0.553333
77 237 0 0.543333
78 239 0 0.633333
79 244 0 0.68
80 251 0 0.606667
81 249 0 0.58
82 245 0 0.823333
83 247 0 0.723333
84 244 0 0.646667
85 244 0 0.576667
86 242 0 0.68
87 252 0 0.926667
88 239 0 0.616667
89 247 0 0.653333
90 244 0 0.546667
91 252 0 0.74
92 247 0 0.56
93 240 0 0.623333
94 243 0 0.66
95 247 0 0.646667
96 249 0 0.66
97 235 0 0.47
98 247 0 0.666667
99 242 0 0.793333
100 248 0 0.796667
- Best solutions are:
0 : 0.0 -> Individual('i', [7, 2, 8, 14, 9, 4, 0, 15, 6, 11, 13, 1, 3, 5, 10, 12])
1 : 0.0 -> Individual('i', [7, 2, 6, 14, 9, 4, 0, 15, 8, 11, 13, 1, 3, 5, 12, 10])
2 : 0.0 -> Individual('i', [7, 2, 6, 14, 9, 4, 0, 15, 8, 11, 13, 1, 3, 5, 10, 12])
3 : 0.0 -> Individual('i', [7, 2, 8, 12, 14, 4, 0, 15, 6, 11, 3, 1, 9, 13, 5, 10])
4 : 0.0 -> Individual('i', [7, 3, 6, 12, 14, 4, 0, 15, 8, 2, 13, 1, 9, 11, 5, 10])
5 : 0.0 -> Individual('i', [7, 13, 6, 1, 14, 4, 0, 15, 8, 11, 3, 12, 9, 2, 5, 10])
6 : 0.0 -> Individual('i', [2, 13, 11, 3, 7, 15, 4, 0, 14, 8, 6, 12, 9, 5, 1, 10])
7 : 0.0 -> Individual('i', [14, 2, 6, 12, 7, 4, 0, 15, 8, 11, 3, 1, 9, 5, 10, 13])
8 : 1.0 -> Individual('i', [2, 13, 6, 12, 7, 4, 0, 15, 8, 14, 3, 1, 9, 5, 10, 11])
9 : 1.0 -> Individual('i', [7, 2, 6, 12, 14, 4, 0, 15, 8, 11, 3, 1, 9, 13, 5, 10])
10 : 1.0 -> Individual('i', [7, 3, 15, 12, 8, 0, 4, 6, 14, 10, 13, 1, 9, 5, 2, 11])
11 : 1.0 -> Individual('i', [7, 3, 6, 12, 14, 5, 0, 13, 11, 2, 15, 1, 9, 4, 10, 8])
12 : 1.0 -> Individual('i', [7, 14, 1, 8, 13, 4, 0, 15, 6, 11, 3, 12, 9, 5, 2, 10])
13 : 1.0 -> Individual('i', [7, 13, 6, 12, 14, 4, 0, 15, 8, 2, 3, 1, 9, 11, 5, 10])
14 : 1.0 -> Individual('i', [2, 13, 6, 12, 7, 4, 0, 15, 8, 10, 3, 1, 9, 5, 14, 11])
15 : 1.0 -> Individual('i', [7, 3, 15, 8, 12, 0, 4, 6, 14, 10, 13, 1, 9, 5, 2, 11])
16 : 1.0 -> Individual('i', [7, 3, 6, 12, 14, 5, 0, 13, 11, 4, 15, 1, 9, 2, 10, 8])
17 : 1.0 -> Individual('i', [7, 2, 12, 14, 9, 4, 0, 15, 8, 11, 13, 1, 3, 5, 10, 6])
18 : 1.0 -> Individual('i', [7, 13, 6, 1, 14, 4, 0, 15, 8, 11, 3, 12, 9, 5, 10, 2])
19 : 1.0 -> Individual('i', [5, 2, 13, 10, 7, 4, 12, 0, 8, 3, 14, 1, 9, 15, 6, 11])
20 : 1.0 -> Individual('i', [7, 5, 8, 12, 14, 4, 0, 15, 6, 11, 3, 1, 9, 13, 10, 2])
21 : 1.0 -> Individual('i', [7, 5, 8, 12, 14, 4, 0, 15, 6, 11, 3, 1, 9, 13, 2, 10])
22 : 1.0 -> Individual('i', [7, 13, 6, 12, 14, 4, 0, 15, 8, 11, 3, 1, 9, 5, 10, 2])
23 : 1.0 -> Individual('i', [14, 13, 6, 12, 7, 4, 0, 15, 8, 11, 3, 1, 9, 5, 10, 2])
24 : 1.0 -> Individual('i', [7, 13, 6, 1, 14, 4, 0, 15, 11, 8, 3, 12, 9, 2, 10, 5])
25 : 1.0 -> Individual('i', [2, 14, 11, 3, 10, 6, 1, 5, 0, 13, 15, 12, 8, 4, 7, 9])
26 : 1.0 -> Individual('i', [7, 2, 6, 12, 14, 4, 0, 15, 8, 11, 3, 1, 9, 5, 10, 13])
27 : 1.0 -> Individual('i', [13, 8, 11, 3, 10, 15, 4, 12, 0, 6, 1, 7, 5, 14, 2, 9])
28 : 1.0 -> Individual('i', [7, 13, 6, 12, 14, 0, 4, 15, 8, 11, 3, 1, 9, 5, 10, 2])
29 : 1.0 -> Individual('i', [7, 3, 8, 12, 14, 4, 0, 15, 6, 10, 13, 1, 9, 5, 2, 11])